geomatria płaska
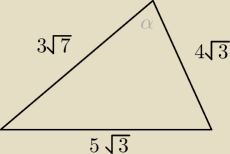
Wiola: Sprawdź, czy trójkąt o bokach 5√3 ,3√7 ,4√3 jest ostrokątny, prostokątny czy rozwartokątny?
6 kwi 14:10
ICSP: Niech a,b,c będą bokami trójkąta i ponadto a < b < c
Wtedy
Trójkąt jest ostrokątny gdy c2 < a2 + b2
Trójkąt jest rozwartokątny gdy c2 > a2 + b2
a prostokątny to wiadomo kiedy.
6 kwi 14:30
Andrzej: Czyli wychodzi (5√3)2=(3√ 7)2+( 4√ 3)2
75=63+48
75=111
c2<a2+b2 czyli trójkąt jest ostrokątny
6 kwi 14:53
Saizou :
5
√3 =
√75
3
√7 =
√63
4
√3 =
√48
Największy kąt leży naprzeciwko najdłuższego boku.
Z tw. cosinusów
(5
√3)
2=(3
√7)
2+(4
√3)
2−2•3
√7•4
√3•cosα
75=63+48−24
√21cosα
| | 36 | |
cosα= |
| > 0 zatem α∊(0; 90o), stąd trójkąt jest ostrokątny. |
| | 24√21 | |
6 kwi 16:04