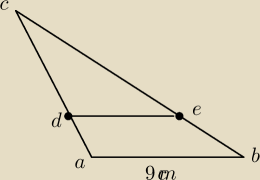
Na rysunku przedstawiono trójkąt ABC, w którym |AB|= 9 a_psik: Na rysunku przedstawiono trójkąt ABC, w którym |AB|= 9 cm oraz odcinek DE równoległy do boku AB trójkąta.

	5
Stosunek pola trapezu ABED do pola trójkąta ABC jest równy		Oblicz długość odcinka DE
	9

wredulus_pospolitus:

	5		√5		√5
stosunek pół:		to stosunek długości boków:		=
	9		√9		3

stąd |DE| = 3√5

an: Zwracam uwagę, że tam jest trapez

Saizou :

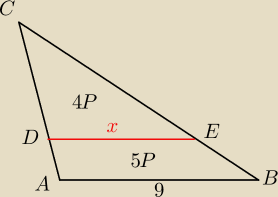
	4P
k2=
	9P

	2
k=
	3

2		x
	=
3		9

x=6 @wredulu się pospieszył z podobieństwiem

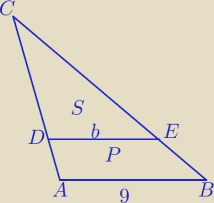Mila: P_ABCDE=P P_ΔDEC=S 1) ΔDEC∼ΔABC z treści zadania:

	P		5		5
		=		⇔ 4P=5S⇔P=		S
	P+S		9		4

	5		9
PΔABC=		S+S=		S
	4		4

PΔDEC		S		4
	=		=		=k2
PΔABC		9   S 4		9

stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa

	2
ΔDEC∼ΔABC w skali k=		⇔
	3

	2		2
b=		|AB|=		*9=6
	3		3

b=|DE|=6 ==================

wredulus_pospolitus: Faktycznie ... nie doczytałem, że to było pole czworokąta

a_psik: Bardzo dziękuję

Eta:

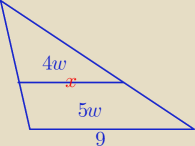
4w		2
	=k2 ⇒ k=
9w		3

	2
x= 9*		⇒ x=6
	3

i po ptokach

Saizou : 19:21 i po ptokach

Eta: Dokładnie