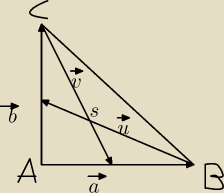
 W trójkącie prostokątnym równoramiennym poprowadzono środkowe z wierzchołków kątów ostrych.
Oblicz cosinus kąta zawartego między nimi.
Na rysunku zaznaczyłem moje oznaczenia.
W trójkącie prostokątnym równoramiennym poprowadzono środkowe z wierzchołków kątów ostrych.
Oblicz cosinus kąta zawartego między nimi.
Na rysunku zaznaczyłem moje oznaczenia.
| 1 | ||
u= − | b + a | |
| 2 |
| 1 | ||
v= − | a + b cosφ wyznaczyłem z iloczynu skalarnego : u . v = |u|*|v|*cosφ | |
| 2 |
| 1 | 4 | |||
Otrzymałem cosφ= | w odpowiedziach jest cosφ= − | |||
| 5 | 5 |
| 4 | ||
otrzymuję cosφ= − | ||
| 5 |
| 1 | 4 | |||
Dlaczego tak się dzieję ? Czy cosφ= | jak i zarówno cosφ= − | są cosinusami kąta | ||
| 5 | 5 |
| 4 | ||
cosφ= | −− φ kąt ostry | |
| 5 |
| 4 | ||
lub cosφ= cos(180o−φ)= −cosφ= − | −− φ kąt rozwarty | |
| 5 |