stereo
jaros:
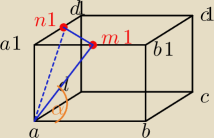
Sześcian ABCDA1B1C1D1 przecięto płaszczyzną AM1N1, gdzie M1 i N1 są środkami boków odpowiednio
A1B1 i A1D1. Udowodnij, że cosinus kąta nachylenia tego przekroju do płaszczyzny podstawy jest
równy .
4 kwi 13:43
Eta:
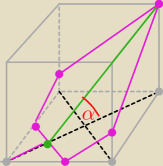
4 kwi 14:03
Eta:
Teraz dasz radę?
Dokończ dyspozycję w treści zadania : "wykaż ...... jest równy ?
4 kwi 14:04
Eta:
Ajjjj sorry
źle przeczytałam treść
4 kwi 14:24
jaros: hmmm czyli twój rysunek jest błędny tak?
4 kwi 14:30
Eta:
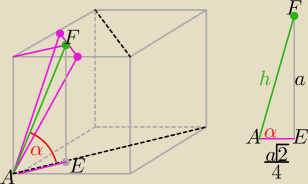h=...
cosα= |AE|/
h=....
4 kwi 14:48
4 kwi 15:18
Eta:
nie
4 kwi 15:28
jaros:
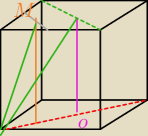
może coś w tych trójkątach?
4 kwi 15:32
Eta:
No przecież wszystko Ci napisałam ! 14:48 o co jeszcze kaman ?
Oblicz h z tw. Pitagorasa
4 kwi 15:34
jaros: Aaaaaa jejku myślałem, ze chodzi o jakaś proporcje... nie zauważyłem tam, że napsialas cos,
| | a√2 | |
dziękuje pięknie, a powiem mi jeszcze, że odcinek IAEI jest równy |
| bo odcinek IAOI |
| | 4 | |
| | a√2 | |
(na moim rysunku) jest równy |
| ? |
| | 2 | |
4 kwi 15:37
jaros: Oki zadanie rozwiązane, Dzękuje jeszcze raz eta
4 kwi 15:45
Eta:
Odp do
15:37 tak
Na zdrowie
A przy okazji jeżeli miałbyś do rozwiązania zadanie ( jak podałam na rys.
14:03
Spróbuj go rozwiązać ,policz cosα w tym zadaniu
4 kwi 15:50