Trójkąt prostokątny o przeciwprostokątnej dlugości 12 obracając się wokół Welma: Trójkąt prostokątny o przeciwprostokątnej dlugości 12 obracając się wokół najdłužszego boku. Jakie wymiary trzeba mieć dziesięć trójkątów, aby uwzględnić bryłę utworzoną w wyniku tego obrotu była największa możliwa?Wyznacz tę objętość. Z góry pięknie dziękuję za pomoc!

wredulus_pospolitus: "Jakie wymiary trzeba mieć dziesięć trójkątów, aby uwzględnić bryłę utworzoną w wyniku tego obrotu była największa możliwa?" <−−− a przetłumaczysz to na jakiś zrozumiały język

wredulus_pospolitus: Czy wiesz jaka bryła powstaje poprzez ten obrót

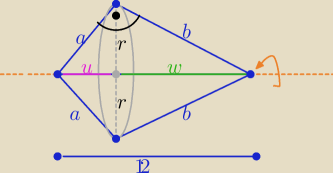
Eta: Bryła składa się z dwóch stożków sklejonych podstawami

	1		1
Vbr=		πr2*u+		πr2*w , u+w=12⇒ w=12−u, u∊(0,12)
	3		3

	1
V=		πr2*(u+w)
	3

V=4πr² r²=u*w ⇒ r²=u(12−u) = −u²+12u V(u)= −4πu²+48πu −− parabola ramionami do dołu osiąga maksimum w wierzchołku

	−48π
umax=		= 6 to w=12−6=6 i r2=36 ⇒ r=6
	−8π

takim trójkątem jest trójkąt prostokątny równoramienny o wymiarach: a=b=6√2 i c= 12 ==============

Welma: Dziękuję bardzo!

Welma: @eta chociaż nie bardzo rozumiem, czemu r²=u*w

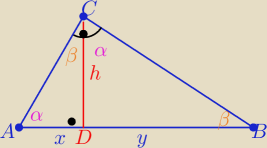
Eta: Z podobieństwa trójkątów ADC i DBC

h		y
	=		⇒ h2=x*y
x		h

Masz ten wzór w karcie wzorów !

Eta: Jasne?

Welma: Jeny, faktycznie! Muszę do matury bardziej zagłębić się w tę kartę. Jeszcze raz bardzo dziękuję!

Eta: Na zdrowie.......łap