Trójkąt równoboczny Klaudia : Na bokach AB, BC i CA trójkata równobocznego ABC o boku długości a obrano odpowiednio punkty K, L i M w taki sposób, że |AK| : |KB|=3:1,|BL| : |LC|=3:1,|CM| : |MA|=2:2. Oblicz pole trójkąta KLM

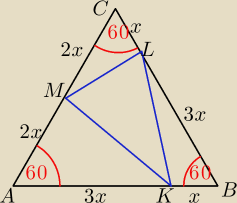
ford: a = 4x

	a2*√3		(4x)2*√3		16x2*√3
PABC =		=		=		= 4x2*√3
	4		4		4

	1		√3
PAKM =		*2x*3x*sin60o = 3x2*
	2		2

	1		3		√3
PKBL =		*x*3x*sin60o =		x2*
	2		2		2

	1		√3
PCLM =		*x*2x*sin60o = x2*
	2		2

P_KLM = P_ABC − P{AKM} − P_KBL − P_CLM

	√3		3		√3		√3
PKLM = 4x2*√3 − 3x2*		−		x2*		− x2*
	2		2		2		2

	5		√3
PKLM =		x2*
	2		2

4x = a

	a
x =
	4

	5		a		√3		5a2*√3
PKLM =		*(		)2*		=
	2		4		2		64

Mila:

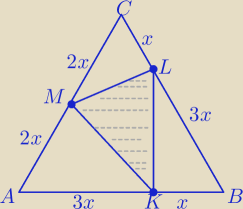
	1
x=		a
	4

	(4x)2√3
PABC=		=4x2
	4

	1		1		1
PKLM=4x2−[		*2x*3x*sin60o+		*x*3x*sin60o+		*x*2x*sin60o}
	2		2		2

P_KLM= licz

Klaudia : Da się to obliczyć bez użycia sinusow? Niestety tego nie mieliśmy jeszcze

Klaudia : Czy jest ktoś w stanie pomóc?

janek191: Można, Pola tych trzech Δ policz ze wzoru P = 0,5 a*h

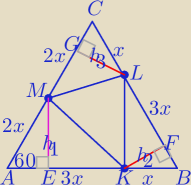Mila: 1)W ΔAEM: (Δekierkowy 90,60,30)

	2x√3
h1=		=x√3
	2

	1		3x2√3
PΔAKM=		*3x*x√3=
	2		2

2)

	x√3
h2=
	2

	1		x√3		3x2√3
PΔKBL=		*3x*		=
	2		2		4

3)

	x√3
h3=
	2

	1		x√3		x2√3
PΔMLC=		*2x*		=
	2		2		2

dalej sama

janek191:

	√3
h = a
	2

Np. Pole Δ AKM P₁ = 0,5*3x*0,5 h itd.

Klaudia : Mila dzięki bardzo

Mila: