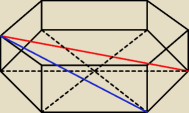
Stereo jaros: Krótsza przekątna graniastosłupa prawidłowego sześciokątnego ma długość 2 a dłuższa przekątna jest nachylona do płaszczyzny podstawy pod katem 45stopni. Oblicz pole całkowite i objętość tego graniastosłupa. Czy krótsza przekątna to ta niebieska?

wredulus_pospolitus: Tak, dokładnie

jaros: Od czego tu zacząć?

jaros: bb

wredulus_pospolitus: krok 1: bok podstawy zapisujesz jako 'a' krok 2: wyznaczasz dłuższą przekątną podstawy krok 3: na podstawię kąta wyznaczasz wysokość graniastosłupa krok 4: wyznaczasz krótszą przekątną podstawy krok 5: z trójkąta z krótszą przekątną graniastosłupa jako przeciwprostokątną, wyznaczasz 'a' krok 6: liczysz P_p ... wstawiasz dane do wzoru na P_c i V

jaros: czyli wyznaczone pole i V będzie z niewiadomom x?

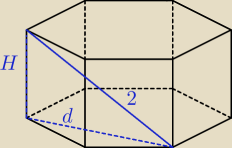
wredulus_pospolitus: co to jest 'x' Bok podstawy Nie ... bo 'x' wyznaczysz z tego trójkąta. bo H masz zależne od 'x' (wyznaczyłeś to z 'większego trójkąta'), d to krótsza przekątna, więc także zależna od 'x'

jaros: Znaczy tak, boki to a, wyznaczyłem H = 2a i teraz mam problem z wyznaczeniem d (jako moje x)

jaros: Czym jest w takim razie to "d" i zrozumiem to zadanie

ford:

	a*√3
d = 2*		= a*√3
	2

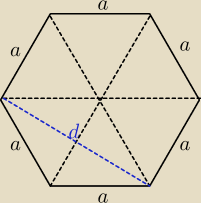
d to dwie wysokości pojedynczego trójkąta równobocznego (w podstawie) o boku a

jaros: aaaaaaa to już rozumiem, dziękuje

wredulus_pospolitus: Albo jak nie zauważyłeś, że d = 2*h_{trójkąta równobocznego o boku a} to możesz z tw. cosinusów. Kąt wewnętrzny sześciokąta to ...

jaros: 60 stopni oczywiście no tak

wredulus_pospolitus: nieee ... 2*60 = 120^o 60^o to masz kąty w tych trójkącikach