prawdopod.
Patryk: Niech A, B ⊂ Ω. Wiedząc, że P(A'∪B') = 0,7 oraz P(A'∩B') = 0,1, oblicz P(A) + P(B)
Prosiłbym o sprawdzenie, mój wynik nie zgadza się z tym w odpowiedziach (powinno wyjść niby
1,2)
P(A'∪B') = P(Ω) − P(AnB) − P(A'nB')
P(AnB) = 0,2
*P(A∪B) = P(A) + P(B) − P(AnB)
P(A'nB') = P(Ω) − P(AnB)
P(A∪B) = 0,9
(*) 0,9 = P(A) + P(B) − 0,2
P(A) + P(B) = 1,1
3 kwi 16:12
wredulus_pospolitus:
pierwsze równanie jest błędne

3 kwi 16:13
wredulus_pospolitus:
P(A'uB') = 1 − P(AnB)

3 kwi 16:13
Patryk: A to nie będzie tak, że P(A'nB') będzie liczone dwa razy i raz trzeba odjąć?
3 kwi 16:22
wredulus_pospolitus:
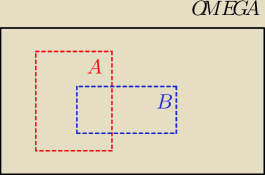
Zaznacz zbiór A'uB'
co jest DOPEŁNIENIEM tego zbioru

Jaki zbiór

3 kwi 16:35
wredulus_pospolitus:
P(A' u B') + P(A n B) = 1
P(A' n B') + P(A u B) = 1
słownie sobie zapisz te zbiory i zauważ, że zachodzą te tożsamości.
3 kwi 16:38
Patryk:
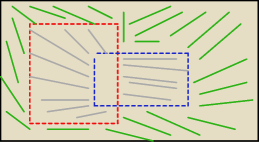
Zielony + szary to A'uB' ale to co na zielono to obszar pochodzący od A' i od B' czyli jest
zliczony jakby dwa razy chyba... Tak samo jak we wzorze na sume AuB gdzie odejmujemy AnB
ponieważ iloczyn zbiorów liczony jest dwa razy
3 kwi 16:55
wredulus_pospolitus:
P(A' u B') <−−− pisząc to oznacza, że RAZ liczysz zielony obszar
gdybyś zapisał jako P(A') + P(B') to wtedy w tym zapisie zielony obszar byłyby
dwukrotnie policzony bo:
a) pierwszy raz w ramach zbioru A'
b) drugi raz w ramach zbioru B'
I dlatego wzór na prawdopodobieństwo sumy zbiorów (w tym przypadku A' i B') wygląda:
P(A' u B') = P(A') + P(B') − P(A' n B')
3 kwi 16:59
wredulus_pospolitus:
zapis
P(A' u B') oznacza:
krok 1: wyznaczamy zbiór A' u B' (tak jak wyznaczyłeś)
krok 2: liczymy prawdopodobieństwo dla tego zbioru
zapis:
P(A') + P(B') oznacza:
krok 1: wyznaczamy zbiór A' (analogicznie do tego co wyznaczyłeś)
krok 2: liczymy prawdopodobieństwo dla tego zbioru
krok 3: wyznaczamy zbiór B' (analogicznie do tego co wyznaczyłeś)
krok 4: liczymy prawdopodobieństwo dla tego zbioru
krok 5: sumujemy otrzymane wartości
I tutaj masz dwukrotne policzenie prawdopodobieństwa dla zbioru A' n B'
3 kwi 17:01
Patryk: Aaaa.... czyli że jesli sumuję używając zapisu ∪ to zbiór pokrywający się liczbę tylko raz a
jak dodaje + zbiory to liczę dwa razy i wtedy trzeba odjąć raz zbiór który policzony został
dwa razy?

3 kwi 17:04
wredulus_pospolitus:
dokładnie

Mam nadzieję, że to już Ci rozjaśniło sprawę i nie będziesz miał w przyszłości już z tym
problemów.
3 kwi 17:06
wredulus_pospolitus:
A teraz podam Ci przykład zastosowania powyższego rozumowania w zadaniu tekstowym
Mam zbiór liczb {1,2,3,...,100}
Wybieramy dwa razy ze zwracaniem po jednej liczbie.
Oblicz prawdopodobieństwo, że przynajmniej jedna z nich jest podzielna przez 3.
Zrób to BEZ metody liczenia prawdopodobieństwa zdarzenia odwrotnego.
3 kwi 17:10
Patryk: Hmm to omega = 100*100
Mogę wylosować {podzielna, podzielna} , {niepodz, podzielna}, {podzielna, niepodz} to liczbośc
zdarzenia:
|A| = 33*33 + 33*67*2 ?
3 kwi 17:28
wredulus_pospolitus:
tak
czyli zauważ, że Ty licząc |A| robisz:
B −−− zdarzenie, że pierwsza jest podzielna przez 3
C −−− zdarzenie, że druga jest podzielna przez 3
liczysz de facto:
|A| = |B n C| + |B / C| + |C / B| = |B n C| + |B| − |BnC| + |C| − |BnC| = |B| + |C| − |BnC|
coś Ci przypomina ten wzór

Ostatnio miałem pytanie związane z tym zadaniem: "dlaczego źle nam wychodzi?" i rozwiązanie
wyglądało analogicznie do tego co napiszę:
A −−− zdarzenie, że pierwsza liczba podzielna przez 3
B −−− zdarzenie, że druga liczba podzielna przez 3
C −−− zdarzenie, że przynajmniej jedna podzielna przez 3 (czyli de facto zbiór A u B)
|A| = 33*100
|B| = 33*100
P(C) = P(A) + P(B) = 2*P(A) = ....
a błąd polegał na tym, że ... dwukrotnie (przy takim liczeniu) został ujęty zbiór AnB czyli
pierwsza i druga podzielna przez 3 (czyli od tego co policzono konieczne byłoby odjęcie |A n
B| = 33*33 )
3 kwi 17:35
Patryk: Hmm głębsza analiza

W każdym razie rozumiem o co chodzi, dzięki wielkie za wytłumaczenie. Na
początku miałem problemy z tymi zbiorami ale po kilku zadaniach rozjaśniło mi się.
Sprawdziłbyś jeszcze jedno zadanko gdybym je wrzucił?
3 kwi 17:44
wredulus_pospolitus:
zawsze możesz też wejść na discorda −−− tam siedzimy z paroma maturzystami i robimy/tłumaczymy
zadania
3 kwi 17:55
Patryk: Jak się nazywasz na Discordzie? Może skorzystam przy okazji

3 kwi 18:50
Patryk: Zaprosiłem Cię
3 kwi 18:55
wredulus_pospolitus: Brzydalos#5694
3 kwi 18:59
ABC:
Jest na Discordzie grupa matematyka.pisz?

3 kwi 19:00
wredulus_pospolitus:
oficjalnej chyba nie ma, ale zrobiliśmy coś a'la grupę i wchodzą maturzyści i coś tam się robi
każdego dnia (arkusze) przy użyciu tablicy on−line −−− głównie Saizou chłopakom tłumaczy
3 kwi 19:02
ABC:
do discorda można podłączyć tablicę online? jest gdzieś w sieci samouczek jak to zrobić?
3 kwi 19:07
salamandra: Nie, każdy wchodzi na tablicę osobno i w czasie rzeczywistym każdy z nas może po niej pisać, a
na discordzie rozmawiamy/piszemy
3 kwi 19:08
wredulus_pospolitus:
/wrzucamy zadania
3 kwi 19:09
wredulus_pospolitus:
Jeżeli przesunął maturę (a raczej − kiedy będzie informacja o przesunięciu matury) to może
któregoś maturzystę wrobię w to by porobić na discordzie trochę działów itd., ale jak narazie
pewnie im by się chciało to robić tak jak i mnie (czyli nie będzie się chciało

)
3 kwi 19:10
Patryk: Chciało by się, chciało, od września po min 5h dziennie matmy robię więc i to wytrzymam

3 kwi 19:14
wredulus_pospolitus:
przesuną*
3 kwi 19:14
ite: ABC jeśli szukasz tablicy online z możliwością rozmów i pisania wiadomości, to draw.chat
to ma.
3 kwi 20:40


 Zaznacz zbiór A'uB'
co jest DOPEŁNIENIEM tego zbioru
Zaznacz zbiór A'uB'
co jest DOPEŁNIENIEM tego zbioru  Jaki zbiór
Jaki zbiór 
 Zielony + szary to A'uB' ale to co na zielono to obszar pochodzący od A' i od B' czyli jest
zliczony jakby dwa razy chyba... Tak samo jak we wzorze na sume AuB gdzie odejmujemy AnB
ponieważ iloczyn zbiorów liczony jest dwa razy
Zielony + szary to A'uB' ale to co na zielono to obszar pochodzący od A' i od B' czyli jest
zliczony jakby dwa razy chyba... Tak samo jak we wzorze na sume AuB gdzie odejmujemy AnB
ponieważ iloczyn zbiorów liczony jest dwa razy

 Mam nadzieję, że to już Ci rozjaśniło sprawę i nie będziesz miał w przyszłości już z tym
problemów.
Mam nadzieję, że to już Ci rozjaśniło sprawę i nie będziesz miał w przyszłości już z tym
problemów.
 Ostatnio miałem pytanie związane z tym zadaniem: "dlaczego źle nam wychodzi?" i rozwiązanie
wyglądało analogicznie do tego co napiszę:
A −−− zdarzenie, że pierwsza liczba podzielna przez 3
B −−− zdarzenie, że druga liczba podzielna przez 3
C −−− zdarzenie, że przynajmniej jedna podzielna przez 3 (czyli de facto zbiór A u B)
|A| = 33*100
|B| = 33*100
P(C) = P(A) + P(B) = 2*P(A) = ....
a błąd polegał na tym, że ... dwukrotnie (przy takim liczeniu) został ujęty zbiór AnB czyli
pierwsza i druga podzielna przez 3 (czyli od tego co policzono konieczne byłoby odjęcie |A n
B| = 33*33 )
Ostatnio miałem pytanie związane z tym zadaniem: "dlaczego źle nam wychodzi?" i rozwiązanie
wyglądało analogicznie do tego co napiszę:
A −−− zdarzenie, że pierwsza liczba podzielna przez 3
B −−− zdarzenie, że druga liczba podzielna przez 3
C −−− zdarzenie, że przynajmniej jedna podzielna przez 3 (czyli de facto zbiór A u B)
|A| = 33*100
|B| = 33*100
P(C) = P(A) + P(B) = 2*P(A) = ....
a błąd polegał na tym, że ... dwukrotnie (przy takim liczeniu) został ujęty zbiór AnB czyli
pierwsza i druga podzielna przez 3 (czyli od tego co policzono konieczne byłoby odjęcie |A n
B| = 33*33 )
 W każdym razie rozumiem o co chodzi, dzięki wielkie za wytłumaczenie. Na
początku miałem problemy z tymi zbiorami ale po kilku zadaniach rozjaśniło mi się.
Sprawdziłbyś jeszcze jedno zadanko gdybym je wrzucił?
W każdym razie rozumiem o co chodzi, dzięki wielkie za wytłumaczenie. Na
początku miałem problemy z tymi zbiorami ale po kilku zadaniach rozjaśniło mi się.
Sprawdziłbyś jeszcze jedno zadanko gdybym je wrzucił?


 )
)
