Prosta i okrąg Getek: Prosta o równaniu y=x+2 przecina okrąg o równaniu (x−3)²+(y−5)²=25 w punktach A i B. Oblicz współrzędne punktów A i B oraz wyznacz równanie stycznej do danego okręgu przechodzącej przez jeden z tych punktów. PRoszę jak by można jeszcze objaśnić jak to rozwiązać.

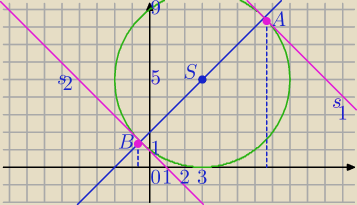
Iryt: 1) y=x+2 (x−3)²+(y−5)²=25 , S=(3,5) (x−3)²+(x+2−5)²=25 ⇔ (x−3)²+(x−3)²=25 2(x−3)²=25

	25
(x−3)2=
	2

	5		5
x−3=		lub x−3=−
	√2		√2

	5√2		5√2
x=3+		lub x=3−
	2		2

	5√2		5√2
y=5+		lub y=5−
	2		2

	5√2		5√2
A=(3+		,5+		)
	2		2

	5√2		5√2
B=(3−		, 5−		)
	2		2

2) Styczna do okręgu przechodząca przez pkt. A Styczna jest prostopadła do promienia w p. styczności A Prosta k: y=x+2 przechodzi przez środek danego okręgu ( sprawdź) Każda prosta : y=−x+b jest prostopadła do prostej k s: y=−x+b i A∊s ⇔

	5√2		5√2
5+		)=−((3+		)+b
	2		2

	10√5
b=8+		=8+5√2
	2

s₁: y=−x+8+5√2 ============== druga styczna : s₂: y=−x+b i B∊s

	5√2		5√2
5−		)=−(3−		)+b
	2		2

	10√2
b=8−		=8−5√2
	2

s₂: y=−x+8−5√2 ============