Rownoleglobok Lena: Dany jest rownoleglobok o kacie ostrym 60°. Odległość punktu przecięcia się przekątnych od bokow rownolegloboku wynoszą 3 i 5. a) Oblicz pole tego rownolegloboku b) Wyznacz długości przekątnych rownolegloboku

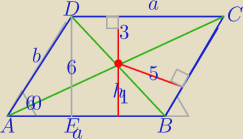
Iryt: h₁=6

	1
|AE|=		b
	2

1)licz długość b 2) oblicz pole 3) oblicz h₂ 4) długości przekątnych z tw. cosinusów

Lena: Jak obliczyć h₂ oraz czy da się obliczyć przekątne w jakis inny sposób, gdyż trygonometrii jeszcze nie miałam

janek191:

	5
P = 6a = 10 b ⇒ a =		b
	3

	√3
6 = b		⇒ b = 4√3
	2

P = 10 b = 40 √3

Iryt:

	b
1) b2=(		)2+62
	2

	b2
b2−		=36
	4

3
	b2=36⇔b2=36*U{4}{3
4

b²=48 b=4√3 2) h₂=10 P=b*h₂=4√3*10=40√3 4) a*h₁=b*h₂ 40√3=a*6

	40√3
a=
	6

	20√3
a=
	3

3) W ΔAED: |AE|=2√3

	20√3		14√3
|EB|=		−2√3=
	3		3

W ΔDEB: h₁²+|EB|²=|DB|²

	14√3
|DB|2=62+(		)2
	3

	196		304		16*19
|DB|2=36+		=		=
	3		3		3

	4√19
|DB|=
	√3

	4√57
|DB|=
	3

============ 4) druga przekątna : AC

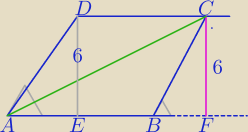
Iryt: c.d 20:42 |BF|=|AE| |AF|=a+|AE|

	20√3		20√3		6√3		26√3
|AE|=		+2√3=		+		=
	3		3		3		3

W ΔAFC:

	26√3
|AC|2=(		)2+62
	3

dokończ

janek191: cd.

	5		5		20√3
a =		b =		*4√3 =
	3		3		3

I AE I = 0,5 b = 2√3

	20√3		14√3
I EB I = a − I AE I =		− 2√3 =
	3		3

Dalej − tw. Pitagorasa