Trójkąt równoboczny Ania: Bok w trójkącie równobocznym jest o a dłuższy od wysokości trójkata. Oblicz pole tego trójkata

ford: x − bok

x*√3
	− wysokość
2

	x2*√3
P =		= ?
	4

	x*√3
x =		+ a
	2

	x*√3
x −		= a
	2

	√3		√3
x(1 −		) = a | : (1 −		)
	2		2

	a
x =
	√3   1 −   2

	a		2a
x =		=		= 2a(2+√3)
	2−√3   2		2−√3

	[(2a(2+√3)]2*√3		4a2(2+√3)2
P =		=		= a2*(2+√3)2
	4		4

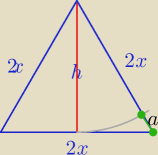Mila: 2x−h=a 2x−x√3=a x*(2−√3)=a /*(2+√3) x=a*(2+√3) 2x=2a(2+√3) P_Δ=a²(2+√3)²*√3 P_Δ=a²*(7+4√3)*√3 P_Δ=(7√3+12)a² ==============

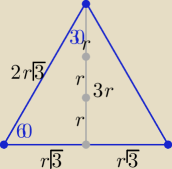Eta: r −− dł. promienia okręgu wpisanego w trójkąt równoboczny 2r√3 −− dł. boku trójkąta , 3r=h, P=3r²√3 z treści zadania

	a(2√3+3)
2r√3−3r=a ⇒ r(2√3−3)=a /* (2√3+3) ⇒ r=
	3

P=a²(2√3+3)²*√3/3 ⇒ P=a²(7+4√3)*√3 P=a²(7√3+12) ============

Eta: