Wyznaczenie prostej na której leży środek okręgu Kamil: Napisz równanie okręgu przechodzącego przez punkt M(0,1) i stycznego do prostych o rownaniach x+y−2=0 i x+y+3=0. Analizowałem rozwiązania tego zadania i nie rozumiem dlaczego środek okręgu, o który się pytają w zadaniu leży na prostej y=−x−0,5? Rozumiem, że odległość od dwóch stycznych równoległych równa jest średnicy i środek okręgu leży na prostej równoległej do obu stycznych która przecina środek odcinka łączącego 2 punkty styczne. Ale dlaczego prosta ta przechodzi równie dobrze przez środek odcinka łączącego punkty (0, 2) i (0, −3)? Nie potrafię sobie tego wyobrazić, przecież ten odcinek ma inną długość niż średnica, przynajmniej tak mi wychodzi z rachunków. Jeśli potrzebny jest rysunek albo moja próba rozwiązania zadania to dodam je później gdy będę miał dostęp do komputera. Chodzi tylko o wyjaśnienie wyznaczenia prostej na której leży środek okręgu, reszta jest dla mnie jasna.

Tadeusz: zauważ, że podane proste sa równoległe

Jerzy: A o co ci tak mniej więcej chodzi ? Skoro okrąg ma być styczny do dwóch prostych równoleglych, to jego środek musi leżeć na prostej, która jest jednakowo odległa od tych prostych.

ICSP: Wybierasz jeden punkt z jednej prostej. Wybierasz drugi punkt z drugiej prostej. Po takim wyborze środek twojego odcinka leży w takiej samej odległości od pierwszej prostej jak i drugiej prostej Co oznacza, że należy do prostej która jest równo odległa od twoich dwóch prostych.

ICSP: ale wcale nie oznacza to, że tak wybrany odcinek jest średnią okręgu.

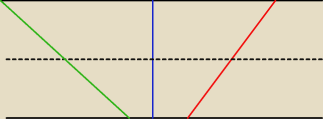
ICSP: Środki wszystkich trzech odcinków leżą na przerywanej prostej, ale tylko odcinek niebieski może być średnicą okręgu

Jerzy: Bo jego połowa, to promień okregu.

Kamil: Już rozumiem. Myślałem po prostu, że prosta między prostymi równoległymi, która jest przecięta przez środek musi być nachylona pod konkretnym kątem, a jeśli nie jest pochylona pod takim kątem to zostaje przecięta w innym punkcie. Wygląda na to, że każda prosta łącząca 2 proste równoległe jest przecięta dokładnie przez środek.