miara kąta
shower: W trójkącie ABC, punkty D oraz E leżą na bokach CA oarz AB tak że BE=6 oraz CD=10. Niech M
oraz N będą odpowiednie środkami odcików BD oraz CE. Ponadto MN=7. Oblicz maiarę kąta BAC.
3 kwi 12:42
Bleee:
Rysunek zrobiony?
3 kwi 13:04
shower:
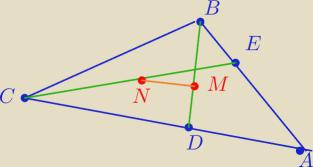
3 kwi 13:15
shower: Jest
3 kwi 13:16
shower: i

3 kwi 16:05
shower : up
3 kwi 17:52
Iryt:
Nic więcej nie ma w treści?
Skąd to zadanie?
3 kwi 19:17
shower: Tak to a pewno cała treść, to zadanie dodatkowe.
3 kwi 23:49
jasnowidz:
shower=
ma...t ?

4 kwi 00:20
shower: co?
4 kwi 08:07
an: 120o
To jest wbrew pozorom proste, ale wymaga przemyślenia dodawanie + Pitagoras,
4 kwi 16:03
shower: Odpowiedz też miałem....
4 kwi 17:04
an:
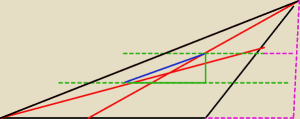
Popatrz na to
4 kwi 17:14
shower: No widze trójkąty prostokątne...
4 kwi 17:26
an: Nie potrafisz powiązać z zadaniem, nie widzisz jak powstaje MN
4 kwi 17:31
shower: jakos nie widze
4 kwi 17:37
an: Popatrz na te przyprostokątne zielone jeżeli je określisz przy pomocy podanych danych i kąta
BAC=α to otrzymasz z Pitagorasa równanie z którego wyznaczysz funkcję trygonometryczną α
i na podstawie jej wartości wartość kąta α.
4 kwi 17:49
Mila:
1) Narysuj prostą równoległą do AB przechodzącą przez punkt N ( K punkt przecięcia z BC)
2) Narysuj prostą do AC przechodzącą przez M i K.
3) Narysuj prostą BN.
Otrzymasz Δ o bokach: .....
dalej sam.
4 kwi 20:39
an: Mila nie rozumiem,jeżeli mogłabyś wyjaśnić to bym prosił. Gdybym z góry (prawie bez obliczeń)
wiedział co z tego wychodzi to narysowałbym trójkąt o bokach 10;12;√364 i jedną środkową 14.
shower doszedłeś do mety, jeżeli tak to czy wiesz jaki wpływ ma długość DA na MN
5 kwi 10:12
an: cd. a właściwie trójkąt bokach 10;6;14 i przedłużył bok 6 jeszcze o 6
mam to co napisałem wyżej i zadanie jest banalne czy można było i na jakiej podstawie
przewidzieć zależność DA i MN, a nie tylko przypuszczać po treści.
5 kwi 10:26
Mila:
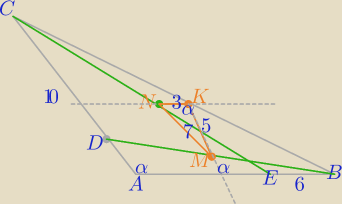 an
an kilka razy rysowałam ten "fikuśny " trójkąt i jeśli widzisz błąd , to pisz.
Pomógł mi Twój wynik (120
o) .
Napisz swoje rozwiązanie.
1) NK|| EB i łączy środki boków ΔEBC (środki CE i CB)
|NK|=3
2) MK||AC
|MK|=5 − odcinek łączący środki boków ΔDBC
3) W ΔMNK:
7
2=3
2+5
2−2*3*5 cos α
49=9+25−30 cosα
15=−30cosα
α=120
0
====
5 kwi 23:28
Mila:
6 kwi 00:06
an:
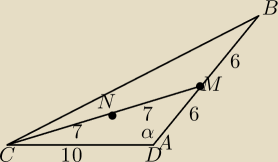
Nie mam zastrzeżeń do Twego rozwiązania
Pierwszy raz rozwiązałem to tak dla uproszczenia zapisu CA=b; 180−α=βwg rysunku 17:14
Składowa pozioma trójkąta prostokątnego (zielony z niebieską przekątną NM}
| | b+6cosβ | | b+12cosβ−10 | |
b+12cosβ− |
| − |
| =5+3cosβ |
| | 2 | | 2 | |
składowa pozioma
Równanie Pitagoras
(5+3cosβ)
2+(3sinβ)
2=7
2
(25+30cosβ+9cos
2β)+(9−cos
2β)=49
30cosβ=15⇒β=60⇒α=120
I doszedłem do wniosku, ze skoro NM nie zależy od długości DA=(0→
∞)
to można to to po prostu rozwiązać zgodnie z rys p/w
Jeżeli DA=0 to
| | 102+62−142 | | 1 | |
cosα= |
| =− |
| ⇒α=120o |
| | 6*10 | | 2 | |
ale chyba coś by tu trzeba dopisać
6 kwi 21:41
Mila:

Dziękuję, to sprowadziło się do cosinusa największego kąta trójkąta podobnego do Δ o bokach :
7,5,3.
6 kwi 22:32



 Popatrz na to
Popatrz na to
 an kilka razy rysowałam ten "fikuśny " trójkąt i jeśli widzisz błąd , to pisz.
Pomógł mi Twój wynik (120o) .
Napisz swoje rozwiązanie.
1) NK|| EB i łączy środki boków ΔEBC (środki CE i CB)
|NK|=3
2) MK||AC
|MK|=5 − odcinek łączący środki boków ΔDBC
3) W ΔMNK:
72=32+52−2*3*5 cos α
49=9+25−30 cosα
15=−30cosα
an kilka razy rysowałam ten "fikuśny " trójkąt i jeśli widzisz błąd , to pisz.
Pomógł mi Twój wynik (120o) .
Napisz swoje rozwiązanie.
1) NK|| EB i łączy środki boków ΔEBC (środki CE i CB)
|NK|=3
2) MK||AC
|MK|=5 − odcinek łączący środki boków ΔDBC
3) W ΔMNK:
72=32+52−2*3*5 cos α
49=9+25−30 cosα
15=−30cosα
 Nie mam zastrzeżeń do Twego rozwiązania
Pierwszy raz rozwiązałem to tak dla uproszczenia zapisu CA=b; 180−α=βwg rysunku 17:14
Składowa pozioma trójkąta prostokątnego (zielony z niebieską przekątną NM}
Nie mam zastrzeżeń do Twego rozwiązania
Pierwszy raz rozwiązałem to tak dla uproszczenia zapisu CA=b; 180−α=βwg rysunku 17:14
Składowa pozioma trójkąta prostokątnego (zielony z niebieską przekątną NM}
 Dziękuję, to sprowadziło się do cosinusa największego kąta trójkąta podobnego do Δ o bokach :
7,5,3.
Dziękuję, to sprowadziło się do cosinusa największego kąta trójkąta podobnego do Δ o bokach :
7,5,3.