Promień okręgu dopisanego Elena:

	a+b+c
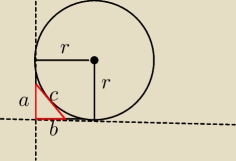
Udowodnij, że promień okręgu dopisanego do przeciwprostokątnej jest równy		.
	2

	a+b−c
Wykazałam, że promień okręgu wpisanego w ten trójkąt równa się		jednak mam problem
	2

z wyznaczeniem promienia okręgu dopisanego. Nie umiem doszukać się tutaj żadnej zależności.. W jaki sposób można wyznaczyć ten promień? Jakaś wskazówka?

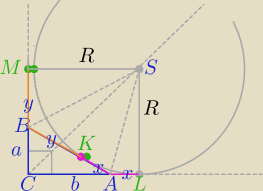Mila: Okrąg dopisany do boku AB trójkąta ABC to okrąg, który jest jednocześnie styczny do tego boku, oraz do przedłużeń boków AC i BC . środek okręgu dopisanego do boku AB leży na przecięciu dwusiecznej kąta C i kątów zewnętrznych K,L,M − punkty styczności x+y=c b+x=R a+y=R b+x+a+y=2R a+b+c=2R

	a+b+c
R=
	2

Elena: dziękuje!