Ciągłość WhiskeyTaster: Mam taki przykład, który nie do końca rozumiem: Wyznaczyć punkty ciągłości f w zależności od c ∊ ℛ f(x, y) = x² + y² dla |x| + |y| ≤ 1 c dla |x| + |y| > 1 (1) f jest ciągła w K₁ = {(x, y) ∊ ℛ²: |x| + |y| < 1}, bo jest wielomianem na tej dziedzinie − to rozumiem, jednomiany są ciągłe, a wielomian to suma jednomianów (2) f jest ciągła na K₂ = {(x, y) ∊ ℛ²: |x| + |y| > 1}, bo f jest funkcją stałą na tej dziedzinie − to też rozumiem Trzeba zbadać f na L = {(x, y) ∊ ℛ²: |x| + |y| = 1} w zależności od c ∊ ℛ. Dla punktów z S¹ wspólnych z L jest f(x, y) = 1, gdzie S¹ to zbiór punktów na okręgu jednostkowym: (1, 0), (−1, 0), (0, 1), (0, −1) − to też rozumiem, są to najprostsze punkty należące do L, gdzie sprawdzamy ciągłość.

	1
Dla okręgu wpisanego w L, f ma stałą wartość		. Punktami styczności są
	2

	1		1
(±		, ±		) − czyli teraz zajmujemy się punktami styczności okręgu o środku w (0,0)
	2		2

	1
oraz promieniu		. Tutaj rozumiem skąd się bierze promień tego okręgu, ale nie bardzo
	√2

rozumiem dlaczego rozpatrujemy akurat te punkty styczności. Na L funkcja f rośnie od B do A (i tak samo od B do C) − i tego już nie widzę. Jak to zobaczyć? Wolałbym bez użycia pochodnej, bo w notatkach nic o tym tutaj nie ma mowy. 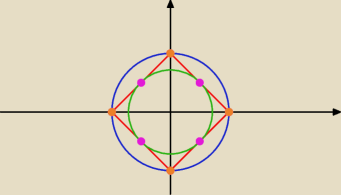Oczywiście to nie koniec zadania, ale nie ma sensu tego tu wklepywać i zabierać czas, bo na dobrą sprawę jeśli uznać powyższe zapisy za prawdziwe, to pozostałe nie stanowią problemu Na pomarańczowo zaznaczyłem punkty styczności zbioru L i okręgu jednostkowego, zaś na różowo

	1
punkty styczności zbioru L oraz okręgu o środku w (0, 0) i promieniu		.
	√2

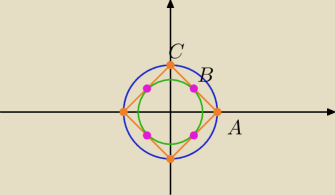WhiskeyTaster: Ojoj, ale gafa, nie oznaczyłem punktów na rysunku

WhiskeyTaster: Mam pewien pomysł: Sprawdźmy na prostej y = −x + 1 wartości funkcji f (bo między innymi na odcinku zawierającym się na tej prostej badamy punkty ciągłości): f(x, −x + 1) = 2x² − 2x + 1, teraz zbadamy pochodną: f'(x, −x + 1) = 4x − 2 = 2(2x − 1).

	1
Pochodna wynosi 0 dla x =		.
	2

Czy w takim razie stwierdzenie, że funkcja od B do C rośnie? W sensie, jeśli faktycznie

	1		1
popatrzeć na to, że w B = (		,		) przyjmuje swoje minimum, to poruszając się po
	2		2

wartościach w kierunku C będzie ona rosła tak, jak to widać na wykresie f(x, −x + 1)?