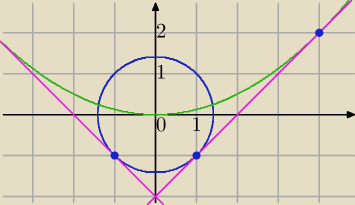
wyznacz równanie wspólnych stycznych 3003: Wyznacz równanie wspólnych stycznych do krzywych x²+y²=2 i 8y−x²=0.

Des: Skąd masz to zadanie? Rachunki mi wychodzą okropne Samo znalezienie punktu na okręgu tak się prezentuje: https://www.wolframalpha.com/input/?i=%28%28%28-4x%2F%28%282-x%5E2%29%5E%281%2F2%29%29%29%5E2%2F8%29%2B%28%282-x%5E2%29%5E%281%2F2%29%29%29%2F%284x%2F%28%282-x%5E2%29%5E%281%2F2%29%29-x%29%3Dx%2F%28%282-x%5E2%29%5E%281%2F2%29%29 Jedna z prostych: y=x−2

Des: W takim lesie jeszcze nie byłem.. może ktoś pokaże łatwiejsze podejście

WhiskeyTaster: A druga nie będzie y = −x − 2? Z symetrii.

Des: Będzie

3003: @Des wydaje mi się, że to jakiś przykładowy arkusz z operonu

Mila:

	1
f(x)=		x2 , g(x)=−√2−x2
	8

1)

	1
f '(x)=		x
	4

	x
g'(x)=
	√2−x2

2) P=(x₀,y₀) − punkt styczności z wykresem funkcji f(x) y=f'(x₀)*(x−x₀)+f(x₀)

	1		1
y=		x0*(x−x0)+		x02⇔
	4		8

	1		1
y=		x0*x−		x02
	4		8

3) Q=(x₁,y₁) − punkt styczności z wykresem funkcji g(x)

	x1
y=		*(x−x1)−√2−x12
	√2−x12

	x1		−2
y=		*x+
	√2−x12		√2−x12

4)

1		x1
	x0=		− jednakowe wsp. kierunkowe stycznej
4		√2−x12

	4x1		1		−2
x0=		i −		x02=
	√2−x12		8		√2−x12

stąd x₁= 1 lub x₁=−1

	4		1
x0=		=4 , f(4)=		*42=2⇔P= (4,2), Q=(1,1)
	√2−1		8

	1
styczna : y=		*4*(x−4)+2
	4

y=x−2 lub x₀=−4, P'=(−4,2),Q'=(−1,1)

	1
y=		*(−4)*(x+4)+2
	4

y=−x−2 ==================

Des: No właśnie, bez pochodnej g(x) chyba się nie obejdzie... pytanie tylko: Skąd maturzysta ma wiedzieć jak się różniczkuje funkcje złożone?

Mila: Q=(1,−1), Q'=(−1,−1)