Rozwiązania na płaszczyźnie
ewa: Cześć, jak rozwiązać takie równanie, bez rozbijania go na milion przypadkow? W sensie chodzi mi
jak najprościej je zapisać by móc zaznaczyć potem w układzie współrzędnych zbiór rozwiązań.
|x|+|y|≤2
2 kwi 16:56
janek191:
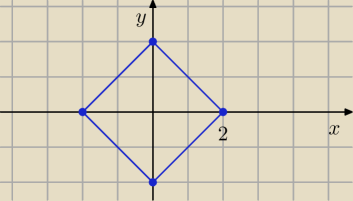
2 kwi 17:04
ford:
pamiętając że |x|+|y|≤a oznacza kwadrat o wierzchołkach (−a,0), (0,−a), (0,a), (a,0)
można od razu zaznaczyć bez rozwiązywania
2 kwi 17:05
ford:
oczywiście dla a>0, bo dla ujemnego a nierówność jest sprzeczna
2 kwi 17:06
ewa: ford, dzięki, czy są jeszcze jakieś takie charakterystyczne związki pomiędzy x a y? Poza tym z
kwadratem
2 kwi 17:13
ewa: W sumie wystarczy się ich nauczyć i pomijamy cały proces liczenia
2 kwi 17:13
ford:
np.
|ax|+|by|≤c dla c>0 to romb o wierzchołkach (−b*c; 0), (b*c; 0), (0; a*c), (0; −a*c)
2 kwi 17:18
ewa: A czy masz może jakiś spis takich związków?
2 kwi 17:36
Mila:
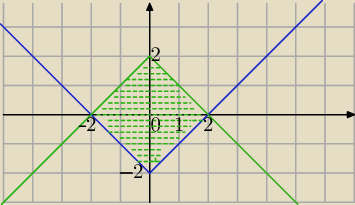
|x|+|y|≤2⇔
|y|≤2−|x|⇔
|x|−2≤y≤−|x|+2
2 kwi 17:51
ICSP: Wystarczy narysować dla x > 0 i y > 0 oraz odpowiednio poodbijać względem osi układu
współrzędnych jak i środka układu.
2 kwi 17:55
ford:
niestety spisu nie mam, tak tylko na poczekaniu wymyśliłem
2 kwi 23:03

 |x|+|y|≤2⇔
|y|≤2−|x|⇔
|x|−2≤y≤−|x|+2
|x|+|y|≤2⇔
|y|≤2−|x|⇔
|x|−2≤y≤−|x|+2