Optymalizacyjne - pole trapezu
szmsz: Jaka powinna być długość podstawy AB trapezu ABCD, aby jego pole było największe, jeśli długość
każdego z pozostałych boków tego trapezu jest równa 10? Oblicz to pole
Z Pitagorasa próbowałem wyznaczyć sobie wysokość ale wyszedł mi ułamek z pierwiastkiem,
| | x2−20x+100 | | 400−x2+20x−100 | | √−x2+20x+300 | |
h = √(100 − |
| )=√ |
| = |
| |
| | 4 | | 4 | | 2 | |
co po podstawieniu do wzoru na pole i wyliczeniu pochodnej dało mi chore równanie.

Czy walnąłem jakiś głupi błąd w obliczaniu wysokości?

Jakaś wskazówka?

szmsz: | | −x(x+10) | | −2x2−10x+100 | |
P'(x) = √100−x2+ |
| = |
| |
| | √100−x2 | | √100−x2 | |
sprawdzam kiedy P'(x)=0
sprawdzam kiedy liczba pod pierwiastkiem w mianowniku jest większa od zera
(10−x)(10+x)>0
x<10 i x>−10
przyrównuję licznik do 0
−2x
2−10x+100=0 /:2
−x
2−5x+50=0
Δ = 25 + 200 = 225
√Δ=15
| | 5−15 | |
x1= |
| =5 (należy do dziedziny) |
| | −2 | |
| | 5+15 | |
x2= |
| =−10 (nie należy do dziedziny) |
| | −2 | |
Funkcja P(x) ma maximum w x=5
P(5) = 15 *
√75 = 15*5
√3=75
√3
Nigdzie się nie pomyliłem?

 Czy walnąłem jakiś głupi błąd w obliczaniu wysokości?
Czy walnąłem jakiś głupi błąd w obliczaniu wysokości?  Jakaś wskazówka?
Jakaś wskazówka? 
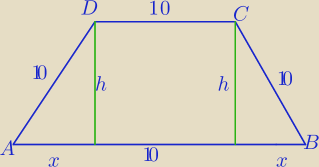 P = 0,5( 2x + 10 + 10)*h = ( x + 10)*h
h = √100 − x2
więc
P(x) = (x + 10)*√ 100 − x2
P = 0,5( 2x + 10 + 10)*h = ( x + 10)*h
h = √100 − x2
więc
P(x) = (x + 10)*√ 100 − x2

