wartość bezwzględna nierówności
japonskiedrzewko77:
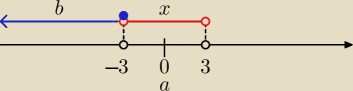
mamy napisać nierówność z wart. bezwzględną typu: "|x − a| > b", "|x − a| < b"
zbiór rozwiązań(przedział): (−3,3)
rozwiązanie wygląda tak: |x − 0| > 3 ⇔ |x| > 3
moje pytanie: dlaczego nie można rozwiązać tego w inny sposób(arytmetycznie chyba również
poprawny?):
|x − 0| > (−
∞,−3)
lub
|x| > (−
∞,−3)
2 kwi 14:01
japonskiedrzewko77: przepraszam, w pierwszym rozwiązaniu jest znak "<"

!
2 kwi 14:02
japonskiedrzewko77: poza tym, czy wartość bezwzględna |x| nie jest mniejsza niż 3

2 kwi 14:04
Jerzy:
Przedział zaznaczony na czerwono, to: |x − 0| < 3
To co ty proponujesz w pierwszym przypadku jest fałszem, a w drugim prawdą dla dowolnego x.
2 kwi 14:07
japonskiedrzewko77: >tak, przedział zaznaczony na czerwono jest zbiorem rozwiązań x i równocześnie |x − 0| < 3
>w pierwszym przypadku czyli: |x − 0| < 3 ⇔ |x| < 3 ? To rozwiązanie z podręcznika.
Chyba, że mówisz o:
|x − 0| > (−∞,−3) ⇔ |x| > (−∞,−3). Jak to prawdą dla dowolnego x? Mógłbyś to rozwinąć?
2 kwi 14:45
 mamy napisać nierówność z wart. bezwzględną typu: "|x − a| > b", "|x − a| < b"
zbiór rozwiązań(przedział): (−3,3)
rozwiązanie wygląda tak: |x − 0| > 3 ⇔ |x| > 3
moje pytanie: dlaczego nie można rozwiązać tego w inny sposób(arytmetycznie chyba również
poprawny?):
|x − 0| > (−∞,−3)
lub
|x| > (−∞,−3)
mamy napisać nierówność z wart. bezwzględną typu: "|x − a| > b", "|x − a| < b"
zbiór rozwiązań(przedział): (−3,3)
rozwiązanie wygląda tak: |x − 0| > 3 ⇔ |x| > 3
moje pytanie: dlaczego nie można rozwiązać tego w inny sposób(arytmetycznie chyba również
poprawny?):
|x − 0| > (−∞,−3)
lub
|x| > (−∞,−3)
 !
!
