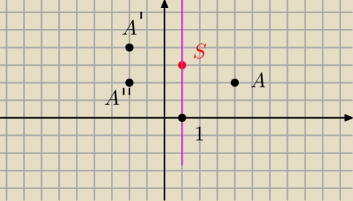
Proszę również o napisanie rozwiązań teddy: 1. Znajdź współrzędne obrazów punktu A=(4,2) w symetrii względem punktu S=(1,3) i w symetrii względem prostej x=1. 2.Wyznacz równanie prostej równoległej do prostej −x+5y−3=0 przechodzącej przez punkt A=(−5,4) 3. Sprawdź czy punkty A=(1,−2), B=(2,−6), C=(−3,6) są współliniowe. 4.Znajdź równanie symetralnej odcinka AB, jeśli: A=(−2,6), B=(2,4). 5.Dla jakiej liczby a proste o równaniach (3a−1)x+y−4=0 oraz 2x+4y−5=0 są prostopadłe? 6.Dany jest trójkąt o wierzchołkach A=(−3,−3), B=(1,5) i C=(0,−5). Wyznacz współrzędne drugiego końca wysokości poprowadzonej z wierzchołka C do boku AB.

teddy: bardzo pilne, proszę o pomoc

ford: Zad. 1 Niech B = (x_B; y_B) − obraz punktu A w sym. względem punktu S C = (x_C; 2) − obraz punktu A w sym. względem prostej x=1

	xA+xB
xS =
	2

	yA+yB
yS =
	2

	4+xB
1 =
	2

	2+yB
3 =
	2

2 = 4+x_B 6 = 2+y_B x_B = −2 y_B = 4 B = (−2; 4) A = (4; 2), S_p = (1; 2), C = (x_C; 2)

	xA+xC
Spx =
	2

	4+xC
1 =
	2

2 = 4+x_C x_C = −2 C = (−2; 2) Zad. 2 −x+5y+C = 0 − szukana prosta A = (−5; 4), więc x=−5, y=4 −(−5)+5*4+C = 0 5+20+C = 0 C = −25 −x+5y−25 = 0 − szukana prosta Zad. 3 prosta AB: y=ax+b {−6=2a+b {−2=a+b {−6=2a+b {2 = −a−b −−−−−−−−−−−−− −4 = a −2 = a+b −2 = −4+b b = 2 AB: y=−4x+2 C = (−3;6) 6 = −4*(−3)+2 6 = 12+2 6 = 14 − nieprawda punkty A, B, C nie leżą na jednej prostej Zad. 4 y = a₂*x+b₂ − szukana symetralna

	yB−yA
a1 =
	xB−xA

	4−6		−2		1
a1 =		=		= −
	2+2		4		2

a₁*a₂ = −1

	1
−		* a2 = −1
	2

a₂ = 2 y = 2x+b₂ − szukana symetralna

	xA+xB
xS =
	2

	yA+yB
yS =
	2

	−2+2
xS =
	2

	6+4
yS =
	2

x_S = 0, y₀ = 5 S = (0; 5) do równania y=2x+b₂ wstawiamy x=0, y=5, wyliczamy b₂ 5=2*0+b₂ 5=b₂ y=2x+5 − szukana symetralna Zad. 5 A₁ = (3a−1) B₁ = 1 A₂ = 2 B₂ = 4 proste są prostopadłe, gdy A₁*A₂+B₁*B₂ = 0 (3a−1)*2 + 1*4 = 0 6a−2 + 4 = 0 6a = −2

	1
a = −
	3

Zad. 6 y = a₂*x+b₂ − prosta zawierająca wysokość poprowadzoną z wierzchołka C C = (0; −5) więc −5 = a*2*0+b₂ zatem −5=0+b₂ b₂ = −5 y = a₂*x−5

	yB−yA		5+3		8
a1 =		=		=		= 2
	xB−xA		1+3		4

a₁*a₂ = −1 2*a₂ = −1

	1
a2 = −
	2

	1
y = −		x−5 − prosta zawierająca wysokość z wierzchołka C
	2

prosta AB: y=a₁*x+b₁ y=2x+b₁ B = (1; 5) więc 5 = 2*1+b₁ b₁ = 3 y = 2x+3 − prosta AB {y = 2x+3

	1
{y = −		x−5
	2

	1
2x+3 = −		x − 5 |*2
	2

4x+6 = −x−10 5x = −16 |:5

	−16
x =
	5

y = 2x+3

	−16
y = 2*(		)+3
	5

	32
y = −		+3
	5

	32		15
y = −		+
	5		5

	17
y = −
	5

	16		17
D = (−		; −		) − szukany drugi koniec wysokości
	5		5

Jerzy:

teddy: strasznie wam dziękuje<3