jak to rozwiązać
Daria: W trójkącie równobocznym o boku a,
różnica promienia okręgu opisanego i promienia okręgu wpisanego równa jest 6.
wówczas:
A. a = 3
B. a = 3√3
C. a = 4√3
D. a = 12
2 kwi 10:09
ford:
w tej książce jest średnicy okręgu opisanego i promienia okręgu wpisanego. Sprawdź
polecenie
2 kwi 10:14
Jerzy:
| | 2 | | a√3 | | 1 | | a√3 | | 36√3 | |
R − r = |
| * |
| − |
| * |
| = 6 ⇔ a√3 = 36 ⇔ a = |
| = |
| | 3 | | 2 | | 3 | | 2 | | 3 | |
12
√3
2 kwi 10:16
Daria: tak średnicy
2 kwi 10:17
Daria: ale nie ma odpowiedzi 12√3
2 kwi 10:20
Jerzy:
Policzyłem różnicę promieni.
2 kwi 10:20
Stefcia:
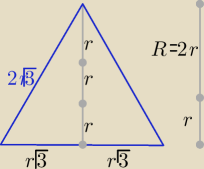
2R−r=6 ⇒4r−r=6 ⇒ r=2
a=2r
√3 ⇒ a=4
√3
========
2 kwi 17:27