Ze zbioru {-2, -1, 0, 1, 2} losujemy... avdava: Ze zbioru {−2, −1, 0, 1, 2} losujemy kolejno bez zwracania liczbę "a" i następnie liczbę "b" i zapisujemy wzór funkcji f(x) = ax+b. Oblicz prawdopodobieństwo zdarzenia, że otrymamy wzór funkcji: a) malejącej b) przyjmującej dla argumentu 0 wartość dodatnią c) stałej d) której wykres przecina oś Oy poniżej początku układu współrzędnych Podpunkt a) i c) zrobiłem wyszło mi 2/5, ponieważ z 5 tych cyfr tylko −2 i −1 są cyframi mniejszymi od zera i z 5 tych cyfr tylko podstawiając 1 cyfrę (0) wyjdzie nam 0x Czy ktoś mógłby mnie nakierować jak zrobić podpunkt b)? Próbowałem pod każdego x podstawić 0 i wyszło mi że tylko w 10 funkcjach z 20 wychodzi wartość dodatnia więc wychodzi 1/2 ale w odpowiedziach jest 2/5 Z góry dziękuję za pomoc

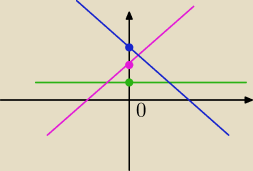
ite: b/ Takie trzy sytuacje nas interesują. Jakie wartości muszą przyjmować a i b w każdej z nich?

avdava: a<0 i b>0 ?

ite: to ta granatowa, a pozostałe?

avdava: a=0 i b>0 w przypadku zielonej a>0 i b>0 w przypadku różowej

ite: widzisz już jaka jest reguła?

avdava: b>0

ite: tak jest : ) f(0)=0*x+b=b, więc dla b>0 również f(0)>0

ite: * f(0)=a*0+b=b

avdava: Czyli można to zapisać w ten sposób?

	1		2		1		2		1		2		1		1
(		*		) + (		*		) + (		*		) + (		*		) +
	5		4		5		4		5		4		5		4

	1		1
(		*		)
	5		4

ite: Czy 22:03 to ma być prawdopodobieństwo zdarzenia, że otrzymamy wzór funkcji przyjmuje dla argumentu 0 wartość dodatnią? Na pewno wynik nie jest taki, ponieważ zawsze prawdopodobieństwo przyjmuje wartości niewiększe od 1. Interesuje nas tylko wartość współczynnika b (a może przyjąć dowolną z podanych wartości). Musi być dodatni. Z pięciu możliwych wyników dodatnie są tylko dwa: 1 i 2. więc P(B) = 2/5

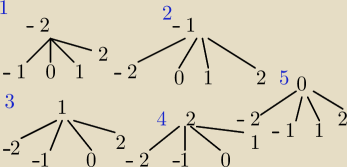
avdava: Też chciałem tak zrobić jak napisałeś, ale co jeśli wylosujemy pierwszą liczbę dodatnią? To wtedy prawdopodobieństwo wylosowania liczby dodatniej (jako drugiej) wynosi już tylko 1/4 bo jedna z dwóch dodatnich została już wylosowana jako pierwsza. (według mnie) Dlatego też narysowałem drzewa i tak: z pierwszego drzewa (szansa na wylosowanie −2 jako pierwszej wynosi 1/5) możemy wylosować dwie dodatnie z czterech (2/4). Z drugiego i piątego drzewa to samo. Natomiast w 3 i 4 drzewie występuje sytuacją, którą opisałem przed chwilą. Prawdopodobieństwo wylosowania cyfry 1 wynosi 1/5, natomiast podczas drugiego losowania, prawdopodobieństwo wylosowania liczby dodatniej (została nam tylko dwójka) wynosi 1/4. Stąd to działanie (22:03). Wychodzi wtedy 8/20 = 2/5. Jeśli takie liczenie jest błędne to proszę o poprawienie i wyjaśnienie. Robię tak ponieważ tak mnie nauczono w szkole.

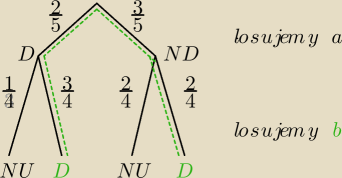
ite: Dopiero po tym osttnim rysunku i zapisie widzę, skąd sie wzięły obliczenia 22:03. Wynik jest poprawny. A nie rysujecie w szkole jednego drzewka dla całego procesu losowania? Jest szyciej. D − zdarzenie polegające na wylosowaniu liczby dodatniej, ND − niedodatniej Wynik 2/5 * 3/4 + 3/5 * 2/4= 2/5

avdava: Niestety nie spotkałem się z czymś takim na lekcjach. Z drzewek głównie niestety nie korzystamy za to bardzo często używamy do tego silni i wzoru Newtona, choć nie widzę potrzeby używania tego w każdym zadaniu skoro są szybkie metody z drzewkami czy nawet jeszcze szybsze − z jednym drzewkiem.

ite: Metoda rysowania nie jest specjalnie szybka: jak będzie wyglądać drzewko dla losowania kolejnych cyfr liczby siedmiocyfrowej (nawet jeśli będziemy rysować tylko gałęzie zdarzeń sprzyjających) ? Tu były dwa etapy, więc rysunek pomaga zobaczyć możliwości. Jakby etapów było więcej, to drzewko by zaciemniało, dlatego korzystacie z uniwersalnej metody czyli stosujecie wzory. Czasem jedna metoda jest lepsza, czasem druga.