Bryły Mariusz: Podstawą ostrosłupa jest trójkąt równoramienny o przyprostokątnej długości 2. Krawędzie boczne ostorsłupa mają długość 2. Jego objętość jest równa?

Mariusz: Pomoże ktoś,wgl nie wiem jak się za to zabrać

wredulus_pospolitus: Trójkąt równoramienny o przyprostokątnej długości 2 Czyli w podstawie jest trójkąt prostokątny równoramienny

wredulus_pospolitus: Skoro wszystkie krawędzie boczne są sobie równe, to znaczy że spodek wysokości tego ostrosłupa jest w punkcie, który jest środkiem okręgu OPISANEGO na podstawie. A gdzie znajduje się środek okręgu opisanego na trójkącie prostokątnym

Mariusz: c²=2²+2² c²=4+4 c²=8 c=2√2 krawędź boczna ma długość 2/3

Mariusz: w połowie przeciwprostokątnej

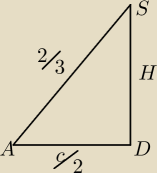
wredulus_pospolitus: więc otrzymujesz taki trójkąt prostokątny (jeżeli 2/3 to krawędź boczna) wyznaczasz H i podstawiasz dane do wzoru na objętość ostrosłupa