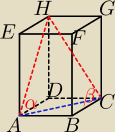
Znajdź cosinus kąta między przekątnymi ścian bocznych prostopoadłościanu. sntr37: Przekątne ścian bocznych prostopadłościanu, wychodzące z tego samego wierzchołka, są nachylone do płaszczyzny podstawy pod kątami α oraz β. Oblicz cosinus kąta między tymi przekątnymi. Próbowałem z twierdzenia cosinusów w trójkącie ΔACH jednak nie potrafię wyrazić boków tego trójkąta tylko i wyłącznie za pomocą funkcji kątów α i β. Prosiłbym o dokładną podpowiedź lub nawet rozwiązanie. Bardzo proszę o pomoc!

Leszek: Kat AHC= δ , δ = 180°−(α +β) cos δ = cos [ 180° − ( α +β )] = cos(α +β) = ........masz taki wzor !

sntr37: Czy kąty HAC i HAD są przystające? Znalazłem różne opinie na temat położenia "kąta między przekątną ściany bocznej a płaszczyzną podstawy".

ite: Panowie, rysunek nie zgadza się z treścią.

sntr37: Tzn?

ite: Przekątne ścian bocznych prostopadłościanu, wychodzące z tego samego wierzchołka, są nachylone do płaszczyzny podstawy pod kątami α oraz β. ↓ β to kąt <HCD a nie <HCA jak na rysunku

Leszek: Kolega @ite ma racje , ja tylko spojrzalem na rysunek i rozwiazalem zadania o tresci , ze te przekatne scian bocznych tworza z przekatna podstawy katy β i α , wiec jest to inna wersja zadania , ale nich taka bedzie do zrobienia dla wprawy !

sntr37: Zadanie jest z próbnej matury od Operonu, na "fejsbukowej" grupie ktoś napisał mi że właśnie tak mają być oznaczone kąty. Na tym zaś forum znalazłem informację że kąty te (HCA i HCD) są takie same.

sntr37: W takim razie ite jak rozwiązać to zadanie?

ite:

	1
|DC|≠		|CA| → cos |<HCD|≠cos|<HCA|
	2

czyli te kąty nie są równe + tym razem fb nie ma racji

ite: na fb taki prima aprilis może... narysuj rysunek z właściwie zaznaczonymi kątami

Leszek: Jezeli nie ma informacji o podstawie prostopadloscianu to wedlug mnie zadanie nie da sie rozwiazac , jezeli np. podstawa jes prostokat to da sie szybko rozwiazac !

sntr37: Nie ma żadnych dodatkowych informacji na temat podstawy więc jest ona prostokątem o dwóch różnych bokach. Jak w takim razie to rozwiązać?

ite: prostopadłościan → podstawą jest prostokąt

sntr37: OK, ale w takim razie jak rozwiązać to zadanie?

ite: Jeśli nikt nie napisze wcześniej, to wieczorem spróbuję. Przyjmij, ze znasz długość boku HD = h, wyznacz AD i DC. Potem wyznacz 1/2 przekątnej AC i np. HC. Jak zapiszesz sinus połowy szukanego kąta za pomocą tych odcinków, to jest nadzieja, że w wyniku h się uprości.

sntr37: Zrobiłem już, wynik wyszedł mi taki:

1   sin alfa

sntr37: Wynik: (w poprzednim poście przypadkowo wysłałem niedokończony )

1   1   [ + − (ctg2α + ctg2β)] *sinα*sinβ   sinα   sinβ
2

sntr37: Wynik jednak błędny, w liczniku w ułamkach z sinα i sinβ obie te funkcje powinny być podniesione do kwadratu, wtedy wynik wychodzi cosγ=sinαsinβ

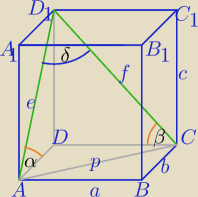
Mila: 1) W ΔADD₁:

	b		b
cosα=		⇔e=
	e		cosα

W ΔCDD₁:

	a		a
cosβ=		⇔f=
	f		cosβ

2) p²=a²+b² p²=e²+f²−2ef cosδ

	b2		a2		b		a
a2+b2=		+		− 2*		*		*cosδ /*cos2α*cos2β
	cos2α		cos2β		cosα		cosβ

	a2tg2β+b2tg2α
cosδ=		* cosα*cosβ⇔
	2ab

	a2   b2   *tg2β+ tgα2 c2   c2
cosδ=		*cosα*cosβ
	a   b   2* *   c   c

	ctg2β*tg2β+ctg2α*tg2α
cosδ=		*cosα*cosβ
	2*ctgβ*ctgα

	2cosα*cosβ
cosδ=		=sinα*sinβ
	2*ctgβ*ctgα

=============================== 2) Jeśli a=b, to α=β cosδ=sin²α

sntr37: Czyli mój wynik jest poprawny czy konieczne byłoby napisanie punktu 2)? Dziękuję za odpowiedź Mila!

ite: A u mnie 16:15 błąd, bo wysokość ΔAHC nie zaczyna się w połowie przekątnej podstawy : (

Mila: Niekoniecznie, zrobiłam to na dwa sposoby i sprawdziłam, czy wg wzoru 18:28 zgadza się dla a=b. Nie masz wyniku z książki?

Mila: Witaj ite, czy mój wynik zgadza się z Twoim? Łatwo o pomyłkę i dlatego pytam

sntr37: Milu tak jak napisałem wcześniej to zadanie jest z próbnej matury Operonu, nie mam do niej odpowiedzi Wynik zgadza się z wynikiem paru innych osób więc raczej jest poprawny.

ite: Witaj Milu, nie doliczyłam do końca, nie mam wyniku. Podaję link do rozwiązań pobrany ze strony Operona. https://arkusze.gieldamaturalna.pl/uploads/6b9cdf9e5837489566a804abf872a9c09f81313e.pdf zad.12

ite: Zadania i rozwiązania 2020 matury próbnej rozszerzonej i podstawowej Operon udostępnia tutaj: https://arkusze.gieldamaturalna.pl/ Może się komuś przyda.

sntr37: Jak już o Operonie mowa to chciałbym pozostawić tutaj wiadomość dla przyszłych maturzystów: Nie kupujcie Vademecum Operonu! Ich zadania/rozwiązania mają wiele błędów!

Mila: Podany tam sposób mniej pracochłonny. Dziękuję za linka.

Micha: Z podanej tresci zadania nie wynika ze podstawa jest prostokatem , moze to byc np.romb i co wtedy ? ?

sntr37: Jest to prostopadłościan. Ścianami (nie tylko bocznymi) prostopadłościanu są prostokąty.