Rzut fizyka syz: Kamień rzucono pod górę o kącie nachylenia 30 do poziomu z prędkością 6 m/s pod kątem 45 do poziomu. W jakiej odległości od miejsca wyrzucenia upadnie ten kamień?

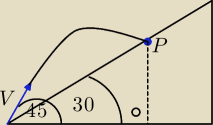
Des: Punkt P(x_p,y_p) w którym ciało zakończy swój lot V=V_xi+V_yj x(t)=x₀+V_xt

	gt2
y(t)=y0+Vyt−
	2

−−−−−−−−−−−−−−−−−

	Vy
sin(45) =		⇒ Vy = Vsin(45)
	V

	Vx
cos(45) =		⇒ Vx = Vcos(45)
	V

Trzeba znaleźć całkowity czas lotu (t_k) ciała: (układ współrzędnych zaczepimy na początku wektora V, to położenie początkowe x₀=0, y₀=0) x(t_k)=x_p=Vcos(45)t_k

	gtk2
y(tk)=yp=Vsin(45)tk−
	2

Z zależności mamy:

	yp
tg(30)=
	xp

y_p=tg(30)x_p czyli x_p=Vcos(45)t_k

	gtk2
tg(30)xp=Vsin(45)tk−
	2

⇒

	gtk2
tg(30)Vcos(45)tk= Vsin(45)tk−		⇒ tk =
	2

Znając czas lotu możesz obliczyć współrzędne punktu P d=odległość od miejsca wyrzucenia d=(x_p² + y_p²)^1₂