Trójkąt w układzie współrzędnych szmsz: Prosta x−y−5=0 zawiera bok AB trójkąta ABC, pr 2x+y−13=0 zawiera bok BC, natomiast prosta 3x−y−7=0 zawiera dwusieczną kąta BAC. Oblicz współrzędne wierzchołków trójkąta ABC oraz wyznacz równanie okręgu opisanego na tym trójkącie. Mam punkty A(1, −4), B(6,1) oraz punkt przecięcia prostej BC z dwusieczną BAC (oznaczyłem jako D) D(4,5) Nie mam pojęcia jak wyznaczyć wierzchołek C. Jakaś wskazówka?

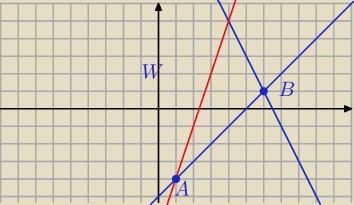
janek191: Wyznacz prostą AC jako obraz prostej AB w symetrii osiowej względem prostej AD ( czerwonej).

janek191: Litera W nie jest potrzebna.

szmsz: wyznaczyłem prostą k prostopadłą do AD przechodzącą przez B

	1
k = −		x+3
	3

i wtedy punkt przecięcia prostej k z prostą AD wyszedł S(3,2) S jest środkiem odcinka BC czyli mam układ równań

6+x
	=3
2

1+y
	=2
2

wyszło C(0,3) Jak obliczyłem sobie długości to wyszło że jest to trójkąt równoramienny. Tak ma być?

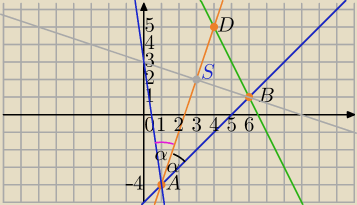
Mila: 1) AB: x−y−5=0⇔ y=x−5 BC: 2x+y−13=0⇔y=−2x+13 3x−y−7=0 zawiera dwusieczną kąta BAC. d: y=3x−7 A=(1,−4) ,B=(6,1), D=(4,5) 2) B' − Punkt symetryczny do punktu B względem AD d' − Prostopadła do AD i przechodząca przez B.

	1		1
y=−		x+b i 1=−		*6+b⇔b=3
	3		3

	1
y=−		x+3
	3

S− punkt przecięcia prostych

	1
−		x+3=3x−7
	3

x_s=3, y_s=2 S=(3,2) − środek BB', B=(6,1)

	x+6		1+y
3=		i 2=
	2		2

B'=(0,3) 3) prosta AC: A=(1,−4) y=ax+3 i −4=a+3⇔ a=−7 y=−7x+3 4) Wsp. punktu C −7x+3=−2x+13 −5x=10 x=−2, y=17 C=(−2,17) Dalej sam

szmsz: dzięki Mila

Mila:

szmsz: Długości boków wyszły |AB| = 5√2 |BC| = 8√5 |AC| = 15√2 wtedy z twierdzenia cosinusów wyznaczyłem sobie cosinus kąta BAC

	3
cosBAC =
	5

z pomocą jedynki trygonometrycznej wyznaczyłem sinus tego kąta

	9		16		4
sinBAC = √1−		=√		=
	25		25		5

i wtedy z twierdzenia sinusów wyznaczam promień okręgu

8√5
	= 2R
4   5

	16√5
R =
	5

Potem muszę wyznaczyć równania symetralnym tych prostych

	1		13
SAC (−		,		)
	2		2

S_BC (2, 9)

	7		3
SAB (		, −		)
	2		2

wyznaczam symetralne k do tych prostych k_AB : y=−x+2

	1		46
kAC: y=		x+
	7		7

	1
kBC: y=		x+8
	2

biorę sobie dwie z tych prostych i je porównuję

	1		46
−x+2=		x+
	7		7

lub

	1
−x+2=		x+8
	2

lub

1		1		46
	x+8 =		x+
2		7		7

x=−4 y=6 równanie okręgu

	16√5
(x+4)2+(y−6)2= (		)2
	5

wszystko się zgadza?

szmsz: ah widzę że promień źle wyliczyłem

szmsz: R = 5√5 i (x+4)²+(y−6)²=(5√5)²

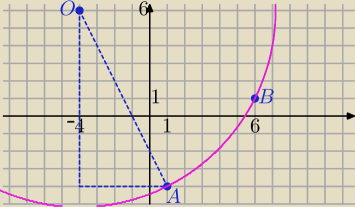
Mila: A=(1,−4) ,B=(6,1), C=(−2,17) środek okręgu opisanego na Δ leży w punkcie przecięcia symetralnych boków. 1) symetralna AB P=(x,y) − dowolny punkt symetralnej AB |AP=|BP| (x−1)²+(y+4)²=(x−6)²+(y−1)²⇔ y=2−x 2) symetralna AC (x−1)²+(y+4)²=(x+2)²+(y−17)²

	1		46
y=		x+
	7		7

3) środek okręgu

1		46
	x+		=2−x
7		7

x=−4, y=6 O=(−4,6), A=(1,−4) r²=|OA|²=(1+4)²+(−4−6)²=25+100 r²=125, r=5√5 (x+4)²+(y−6)²=(5√5)²

szmsz: dzięki wielkie

Mila: