trójkat nieumiem: Średnica okręgu opisanego na trójkacie ABC wynosi 25. Długości AB, BC, CA są liczbami naturalnymi oraz AB > BC. Odległości od środka tego okręgu do boków AB, BC są też liczbami naturalnymi. Oblicz obwód tego trójkata.

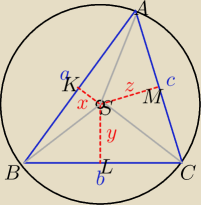
ford: Punkt przecięcia symetralnych boków trójkąta jest środkiem okręgu opisanego na trójkącie Czerwone odcinki (odległości od środka okręgu do boków) narysowane linią przerywaną zawierają się w symetralnych boków trójkąta Zatem K, L, M są środkami boków AB, BC, AC z tw. Pitagorasa

	a		25
(		)2 + x2 = (		)2
	2		2

	b		25
(		)2 + y2 = (		)2
	2		2

	c		25
(		)2 + z2 = (		)2
	2		2

Rozważając jedno z tych równań, mamy

a2		625
	+ x2 =
4		4

a² + 4x² = 625 a² = 625 − 4x² a² = (25−2x)(25+2x) Metodą prób i błędów dobieramy x, aby liczba (25−2x)(25+2x) była kwadratem liczby naturalnej x = 10, wówczas a² = (25−20)(25+20) = 5*45 = 225, stąd a = 15 x = 12, wtedy a² = (25−24)(25+24) = 1*49, stąd a = 7 i to są tylko dwa przypadki liczb x, dla których a jest naturalne warunek AB > BC powoduje, że a>b

	a		25
bez straty ogólności można założyć, że rozwiązaniami równania (		)2 + x2 = (		)2
	2		2

są a=15, x=10

	b		25
zaś rozwiązaniami równania (		)2 + y2 = (		)2 są b=7, y=12
	2		2

	c		25
Ze względu na równanie (		)2 + z2 = (		)2 mamy dwie możliwości: c = 15 lub c = 7
	2		2

Jednak dla c = 7 mamy a=15, b=7, c=7 więc nierówność trójkąta nie jest spełniona. Zostaje c = 15. Wówczas a+b+c = 15+7+15 = 37

nieumiem: Ja mam w odpowiedzi że 42