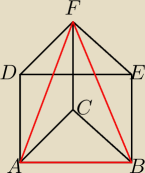
Stereo więcej Nieogarnięty: Podstawą graniastosłupa prostego jest trójkąt o bokach długości |AB|=3 |BC|=2 |AC|=√7. Przez najdłuższy bok podstawy i jeden z wierzchołków drugiej podstawy poprowadzono płaszczyznę. W przekroju otrzymano trójkąt o polu 3√3. Oblicz cosinus kąta między ramionami tego trójkąta oraz miarę kąta zawartego między płaszczyzną przekroju a płaszczyzną podstawy. I nie mam kompletnie pomysłu na to dziwo.

Nieogarnięty: Ma ktoś jakiś pomysł?

ford: załóżmy że punkt G leży gdzieś na odcinku AB, oraz FG będzie wysokością tego czerwonego trójkąta oblicz wysokość FG z pola ABF Oznacz |FC| = H (wysokość graniastosłupa) oznaczasz |AG| = x, |GB| = 3−x robisz układ równań z Pitagorasów w ΔAGF i ΔFGB wyliczasz x i H na koniec tw. cosinusów dla ΔABF

ford: *jeszcze zanim układ równań z ΔAGF i ΔFGB to z Pitagorasa w ΔACF i ΔCBF wyliczasz że |AF| = √H²+7 oraz |BF| = √H²+4

Nieogarnięty: Oki, dzięki