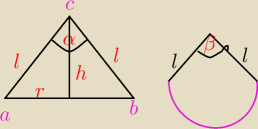 Kąt rozwarcia stożka ma miarę α. Oblicz miarę łukową kąta środkowego rozwiniętej powierzchni
bocznej tego stożka.
Nie rozumiem o co tu chodzi kompletnie
Kąt rozwarcia stożka ma miarę α. Oblicz miarę łukową kąta środkowego rozwiniętej powierzchni
bocznej tego stożka.
Nie rozumiem o co tu chodzi kompletnie
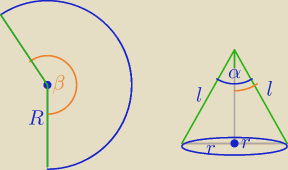 Powierzchnia boczna stożka powstaje z pewnego wycinka koła o promieniu R=l i takim kącie β,
że Pb=Pw
Powierzchnia boczna stożka powstaje z pewnego wycinka koła o promieniu R=l i takim kącie β,
że Pb=Pw
| β | ||
1) Pw= | πR2 | |
| 360 |
| β | |
πR2=π*r*l, l=R | |
| 360 |
| β | |
R2=r*R | |
| 360 |
| β | ||
r= | R | |
| 360 |
| β | ||
r= | *l /:l | |
| 360 |
| r | β | ||
= | |||
| l | 360 |
| α | β | |||
sin | = | |||
| 2 | 360 |
| α | ||
β=360o*sin | ||
| 2 |
| r | |
= sin 0,5α ⇒ r = l sin 0,5α | |
| l |
| β | L | 2π l sin 0,5α | |||
= | = | = sin 0,5α | |||
| 2π | 2π l | 2πl |
