Odległość środka symetrii

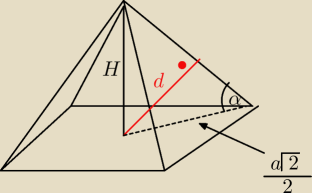
Odległość środka symetrii kolka: Odległość środka symetrii podstawy ostrosłupa czworokątnego prawidłowego od krawędzi bocznej tego ostrosłupa jest równa d, a kąt nachylenia tej krawędzi do płaszczyzny podstawy jest równy α.Oblicz pole powierzchni bocznej i objętość tego ostrosłupa.

31 mar 00:19

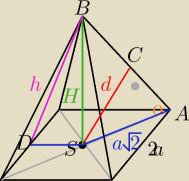
Saizou : rysunek

w ΔSAC

	d
sinα=		→a=...
	a√2

w ΔSAB

	H
tgα=		→H=...
	a√2

V=P_p*H w ΔDSB Pitagoras → h

	1
P_b=		2ah
	2

31 mar 00:34

Saizou : I dopiszę jeszcze, że DS=a

31 mar 00:35

salamandra: rysunek

d

sinα=

a√2 
2 

a√2
	*sinα=d
2

	2d		2d√2		d√2
a√2=		⇒ 2a=		⇒ a=
	sinα		sinα		sinα

H

tgα=

a√2 
2 

	a√2
tgα*		=H
	2

	d
tgα*		=H
	sinα

	tgα*d
H=
	sinα

	1		2d²		1		2d³*tgα
V=		*		=		*
	3		sin²α		3		sin³α

Jeśli chodzi o objętość to chyba tak to będzie

31 mar 00:40

salamandra: o, już się spóźniłem...

31 mar 00:40

Saizou : Warto ćwiczyć, wynik można jeszcze uprościć. Podziałaj na tgα i sinα

31 mar 00:47

salamandra:

1

 sinα 
2d3*
 cosα 

 1 
2d3*
 cosα 

2d3

*

=

=

3

sin3α

sin2α

cosα*sin2α

31 mar 00:50

Saizou : emotka

31 mar 00:55