Optymalizacja ala: Trójkąt prostokątny o przeciwprostokątnej 12 obraca się wokół najdłuższego boku. Jakie wymiary powinien mieć ten trójkąt, aby objętość tej bryły była największa? Wyznacz tę objętość.

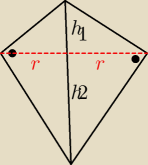
salamandra: h1+h2=12

salamandra: Na pewno masz tylko tyle danych?

ala: tak:( nic więcej

ala: wiec nie da się tego policzyć tylko z tych danych

Szkolniak: Bryła składa się z dwóch stożków. h₁+h₂=12 ⇒ h₂=12−h₁ r=h=√h₁*h₂=√h₁(12−h₁) Objetość górnego stożka:

	h12(12−h1)
V1=		*π
	3

Objętość dolnego stożka:

	π
V2=		*h1(12−h1)2
	3

V=V₁+V₂=... tworzysz funkcję i szukasz maximum lokalnego.. może o to chodzi?

Mila:

	1
V=		*πr2*12
	3

h₁=x, h₂=y r²=x*y x+y=12 y=12−x⇔r²=x*(12−x), x∊(0,12)

	1
V(x)=		π*x*(12−x)
	3

	π
V(x)=		*(12x−x2)
	3

Licz dalej sama

salamandra: Milu, r²=x*y to z własności, że jeżeli wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną na odcinki o długościach x i y, to h²=xy?

Mila: Tak

salamandra: właśnie jak zacząłem niedawno przerabiac planimetrię z Kiełbasy to we wstępie była przytoczona ta zależność, ale jakoś nigdy z niej nie było mi dane skorzystać