matura
Saizou :
Dla maturzystów

Zad 1
Pierwiastkami wielomianu w o współczynnikach całkowitych są liczby −3, −2 i −1.
Wykaż, że dla dowolnej liczby naturalnej n liczb w(n) jest podzielna przez 6.
30 mar 20:21
Szkolniak: Pierwiastkami wielomianu są 3 kolejne liczby całkowite, zatem jedna z nich jest na pewno
podzielna przez 2 i jedna jest na pewno podzielna przez 3 − stąd liczba ta podzielna jest
przez 6.
30 mar 21:14
Saizou : 
Zad 2
Ze zbioru liczb {1, 2, ..., 2010} losujemy jedną liczbę.
Oblicz prawdopodobieństwo tego, że wybrana liczba nie jest podzielna przez 6
ani przez 15
30 mar 21:16
Szkolniak: Obliczę zdarzeniem przeciwnym.
A − wylosowanie liczby podzielnej przez 6 lub przez 15
|Ω|=2010
podzielne przez 6
6, 12, 18,...
liczby te tworzą ciąg arytmetyczny o wzorze ogólnym: a
n=6n
6n≤2010
n≤335 → jest 335 takich liczb
podzielne przez 15
15, 30, 45,...
liczby te tworzą ciąg ar. o a
n=15n
15n≤2010
n≤134 → takich liczb jest 134
Powtarzające się liczby: 30,60,90,...
To samo rozumowanie i takich liczb jest 67.
| | 335+134−67 | | 1 | |
P(A)= |
| = |
| |
| | 2010 | | 5 | |
| | 4 | |
Prawdopodobienstwo tego że wybrana liczba nie jest podzielna przez 6 ani 15 jest równa |
| . |
| | 5 | |
30 mar 21:26
Saizou : 
Zad 3
W stożek o wysokości 8 wpisano kulę. Punkt styczności kuli ze stożkiem podzielił
tworzącą stożka w stosunku 2:3. Oblicz promień kuli.
30 mar 21:34
Patryk: Szkolniak, chcesz fajne zadanko?

30 mar 21:35
Szkolniak: Patryk wrzuć

30 mar 21:36
Patryk: Osobiście powiem, że jest czasochłonne, sam robiłem je ze 30 min
Rozwiąż nierówność 1 + log2(sin2x) + log22(sin2x) + .....<0,(6) w zbiorze <0; 2π> gdzie lewa
strona nierówności jest szeregiem geometrycznym zbieżnym
30 mar 21:41
Patryk: Szczególnie fajna sprawa z założeniami

30 mar 21:43
Adamm:
1.
w(n) ≡ w(x) = 0 (mod 3), gdzie x∊{−1, −2, −3}
w(n) ≡ w(x) = 0 (mod 2), gdzie x∊{−1, −2}
⇒
w(n) ≡ 0 (mod 6)
zatem
6|w(n) dla każdego n∊Z
30 mar 21:48
jaros: Wiem, że temat do rozwiązania jednak chciałbym się spytać, czy uważacie że matury bedą
przesunięte?
30 mar 21:49
Patryk: Na stówkę będą, nie ma opcji żeby odbyły sie w maju
30 mar 21:49
Saizou :
Patryk nie jest takie złe
1−log2(sin(2x)) jest dodatnie
30 mar 21:50
jaros: @Saizou a ty jak sądzisz?
30 mar 21:57
Szkolniak:
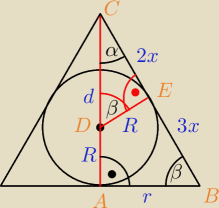
|AC|=h=8
|CD|=d=8−R
zΔ
DEC:
| | 1 | |
4x2+R2=R2−16R+64 ⇒ R=4− |
| x2 |
| | 4 | |
ΔDEC~ΔBAC (cecha kkk), zatem:
| | 2x | | 8 | | 32−4R | |
|
| = |
| ⇒ x2= |
| |
| | 8−R | | 5x | | 5 | |
| | 1 | |
Podstawiamy pod 'x2' w 'R=4− |
| x2' i R=3. |
| | 4 | |
30 mar 21:57
Saizou :
Powiem tylko tak: Oceniając posunięcia ludzi u władzy niczego nie można być pewnym.
Na tym zakończę może przypuszczenia co będzie.
PS. Uczcie się tak jak by matury miałby być w terminie.
I pamiętajcie: umiesz liczyć, licz na siebie

30 mar 21:59
Saizou :
Szkolniak w 80% dobrze, brakuje drugiego przypadku.
30 mar 22:00
Szkolniak: Drugi? Jaki drugi?

30 mar 22:02
Saizou :
zastanów się na tym stosunkiem
30 mar 22:03
jaros: Czemu |CD|=d=8−R a nie |CD|=d=8−2R?
30 mar 22:03
Szkolniak: drugą opcję miałbyś gdybym ten odcinek zaznaczył od wierzchołka 'C' do tego najwyższego punktu
kuli, ja zaznaczyłem do środka
30 mar 22:09
Saizou :
|CD|=8−|DA|
Od całej wysokości odejmujesz R na dole
30 mar 22:09
Szkolniak: Saizou chodzi po prostu o to że musiałbym zamienić miejscami '2x' i '3x'?
30 mar 22:13
Saizou :
Dokładnie

a teraz zadanie
Patryka
30 mar 22:16
Saizou :
Adamm ładnie tylko teorii pierścieni nie ma w LO

30 mar 22:27
Adamm:
Alternatywnie.
w(n) = (n+1)(n+2)(n+3)q(n) dla pewnego wielomianu q, a 6|(n+1)(n+2)(n+3)
30 mar 22:36
Szkolniak: a
1=1 ∧ q=log
2(sin2x)
Założenia:
|log
2(sin2x)|<1 ∧ sin2x>0
log
2(sin2x)≠−1 ∧ log
2(sin2x)≠1 ∧ sin2x>0
| | π | | π | | π | |
te 3 założenia spełnione są dla: x∊<0; |
| )∪( |
| ; |
| ) |
| | 4 | | 4 | | 2 | |
| 1 | | 2 | |
| < |
| /*3(1−log2(sin2x)) |
| 1−log2(sin2x) | | 3 | |
| | 1 | |
log2(sin2x)<− |
| , bo (1−log2(sin2x))>0 dla x∊R |
| | 2 | |
t=2x
| | π | | 3 | | π | | π | | π | |
x∊<0; |
| )∪( |
| π;π> ∧ x∊<0; |
| )∪( |
| ; |
| ) |
| | 8 | | 8 | | 4 | | 4 | | 2 | |
| | π | | 3 | | π | |
Odpowiedź: x∊<0; |
| )∪( |
| π; |
| ) |
| | 8 | | 8 | | 2 | |
30 mar 22:43
Saizou :
Jak się nie kopnąłem
| | π | | π | | 3 | | 5 | |
x∊( |
| ; |
| ) ∪ ( |
| π; |
| π) ∪ |
| | 12 | | 8 | | 8 | | 12 | |
| | 13 | | 9 | | 11 | | 17 | |
∪ ( |
| π; |
| π) ∪ ( |
| π; |
| π) |
| | 12 | | 8 | | 8 | | 12 | |
30 mar 23:07
Patryk: Źle, na początku... założenie wyszło nieprawidłowe
30 mar 23:09
Patryk: Saizou dobrze masz

30 mar 23:09
Szkolniak: I już chyba nawet wiem skąd ta głupota w założeniu.. tak to jest jak sie chce na skroty a
wychodzi na to że to nie to samo

30 mar 23:15
30 mar 23:17
30 mar 23:22
Szkolniak: Dzięki

chyba rzeczywiście lepiej sobie to rysować, bo znów próbowałem bez rysunku i ciężko
30 mar 23:47
Saizou :
porady rysunek bardzo pomaga

30 mar 23:51
Saizou : *porządny
30 mar 23:51
Patryk: Jak określałeś tą dziedzinę na rysunku? Bo ja najpierw liczyłem dla 2x, później przeliczałem
dla x i dopiero wtedy zaznaczałem wartości na rysunku
30 mar 23:54
Saizou :
Rysunek przedstawia sin2x
| | 1 | | π | | π | |
sin t = |
| dla t= |
| →x= |
| |
| | 2 | | 6 | | 12 | |
itd.
Zad 4
Oblicz miarę kąta między stycznymi do okręgu x
2+y
2+2x−2y−3=0
poprowadzonymi przez punkt A=(2,0).
30 mar 23:59
salamandra: −2a=2
a=−1
−2b=−2
b=1
S=(−1,1)
r=
√1+1+3=
√5
Równanie prostej AS
A=(2,0) S=(−1,1)
y=ax+b
0=2a+b / *(−1)
1=−a+b
0=−2a−b
1=−a+b
1=−3a
Styczna jest prostopadła do tej prostej i przechodzi przez punkt A, więc jej współczynnik
kierunkowy to: a=3
y=3x+b
A=(2,0)
0=3*2+b
b=6
y=3x+6
Do tej pory ok?
31 mar 00:07
salamandra: A nie, ten punkt nie należy do okręgu
31 mar 00:08
Patryk: Czyli, że cały czas jechałeś na wartościach dla 2x, a dopiero na końcu przy ostatecznym wyniku
zamieniałeś z 2x −−−> na x? Tak mniej pisania
31 mar 00:10
Saizou :
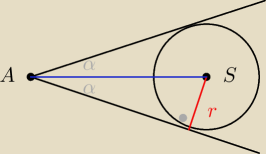
Czasu na maturze Ci zabraknie

MOżna prościej
|AS|=...
sinα=...
31 mar 00:10
salamandra: Myślałem ze ten punkt leży na okręgu i dlatego tak poleciałem
31 mar 00:11
Saizou :
Jak zrobisz rysunek sin(2x), to masz prawie wszystko na tacy podane.
zauważ, że mamy 4 warunki (3 z założeń i jedno z rozwiązania).
wszystkie tyczą się sin(2x) wiec lepiej od razu go narysować.
31 mar 00:13
salamandra: Skąd wynika ze AS będzie dwusieczna kata miedzy stycznymi, te styczne są symetryczne?
31 mar 00:15
salamandra: Wiem ze odległość do punktu styczności jest równa na pewno,. Z tw o odcinkach stycznych
31 mar 00:16
Saizou :
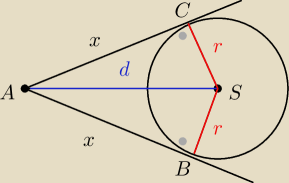
Pokaż, że te trójkąty ABS i ACS są przystające.
31 mar 00:23
salamandra: nie ma co pokazywać

już jasne

31 mar 00:29
Saizou :
Najprostsze dowody są najtrudniejsze

31 mar 00:35
Saizou : Teraz dokończ zadanie

31 mar 00:36
Patryk: To trzeba nawet na maturze pokazywac ze trójkąty są przystające? Nie.mozna po prostu napisac?
Przeciez jakby człowiek mial wszystko dowodzic I pokazywac na każdym kroku to czasu na maturze
na bank zabraknie... zawracanie gitary
31 mar 00:45
salamandra:
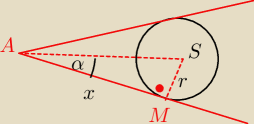
coś w tym jest

r=
√5
r
2+x
2=|AS|
2
|AS|
2=(−1−2)
2+1
2=10
|AS|=
√10
5+x
2=10
x
2=5
x=
√5
(nie wiem w sumie po co to wyliczyłem, ale niech już zostanie)
coś mi tu nie gra
31 mar 00:46
salamandra: aaa, AS=
√10 a nie
√5
| | √5 | | √50 | | 5√2 | | √2 | |
sinα= |
| = |
| = |
| = |
| |
| | √10 | | 10 | | 10 | | 2 | |
więc α=45, to 2α=90
31 mar 00:47
Saizou :
Patryk nie trzeba, nie w takich przypadkach, bo to jest bardzo znana własność.
31 mar 00:50
salamandra: Nadal źle?
31 mar 00:54
Saizou : Jets okej, coś innego zobaczyłem

31 mar 00:55
Saizou :
Zad 5
Promień okręgu wpisanego w trójkąt o bokach 5 i 8 jest równy równy √3 ,
a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.
31 mar 01:00
f123: @Saizou cos latwe zadania podrzucasz, moze wrzuce tutaj to co robilem z wredulusem dzisiaj...
Moze byc ciekawie dla maturzystow

31 mar 01:02
salamandra: Ja już pasuje na dziś, powodzenia f123

jutro można coś się na discordzie złapać i porobić
31 mar 01:06
Saizou :
f123 nie można cały czas trudnych rzeczy robić, bo się maturzyści zniechęcą.
31 mar 01:06
f123: @salamandra mozna jak najbardziej, prawdopodobienstwo dalej czy poszukac ciekawrych zadan
maturalnych ktore warto omowic?
31 mar 01:07
Patryk: Salamandra, skąd ten nick tak w ogóle? Grało się w Wiedźmina?

31 mar 01:07
Saizou :
Tak swoją drogą f123 pamiętałbyś o 2 przypadku w zadaniu 3 ?
31 mar 01:08
f123: @Saizou ktore to zadanie 3

31 mar 01:09
Saizou :
z 21:34
31 mar 01:09
salamandra: f123, możesz jakieś ciekawe z tych arkuszy co robiłeś, ale tez takie nie za trudne, bo te
„schematyczne” tez warto utrwalić.
Patryk− szczerze? Tylko tu go używam, jak pierwszy raz na forum wszedłem to nie wiedziałem jaki
ustawić, bo myślałem ze wchodzę jednorazowo... No i tak zostało

31 mar 01:09
Qn: Zad 5
Korzystając ze wzoru P=1/2r(a+b+c) i wzoru Herona na pole mamy
2 √3 (c + 13) =√−(c2 − 169) (c2 − 9)
Podnoszą do kwadratu i dzieląc przez c+13 mamy c3 − 13 c2 + 3 c + 273 = 0
273:7=39
(c − 7) (c2 − 6 c − 39) = 0
c=7
31 mar 17:44
Saizou :

jeszcze należy pokazać, że trójmian kwadratowy nie ma pierwiastków naturalnych.
31 mar 18:18
Qn: Wystarczy obliczyć delte i już widac...
31 mar 18:20
 Zad 1
Pierwiastkami wielomianu w o współczynnikach całkowitych są liczby −3, −2 i −1.
Wykaż, że dla dowolnej liczby naturalnej n liczb w(n) jest podzielna przez 6.
Zad 1
Pierwiastkami wielomianu w o współczynnikach całkowitych są liczby −3, −2 i −1.
Wykaż, że dla dowolnej liczby naturalnej n liczb w(n) jest podzielna przez 6.
 Zad 2
Ze zbioru liczb {1, 2, ..., 2010} losujemy jedną liczbę.
Oblicz prawdopodobieństwo tego, że wybrana liczba nie jest podzielna przez 6
ani przez 15
Zad 2
Ze zbioru liczb {1, 2, ..., 2010} losujemy jedną liczbę.
Oblicz prawdopodobieństwo tego, że wybrana liczba nie jest podzielna przez 6
ani przez 15
 Zad 3
W stożek o wysokości 8 wpisano kulę. Punkt styczności kuli ze stożkiem podzielił
tworzącą stożka w stosunku 2:3. Oblicz promień kuli.
Zad 3
W stożek o wysokości 8 wpisano kulę. Punkt styczności kuli ze stożkiem podzielił
tworzącą stożka w stosunku 2:3. Oblicz promień kuli.



 |AC|=h=8
|CD|=d=8−R
zΔDEC:
|AC|=h=8
|CD|=d=8−R
zΔDEC:


 a teraz zadanie Patryka
a teraz zadanie Patryka



 chyba rzeczywiście lepiej sobie to rysować, bo znów próbowałem bez rysunku i ciężko
chyba rzeczywiście lepiej sobie to rysować, bo znów próbowałem bez rysunku i ciężko

 Czasu na maturze Ci zabraknie
Czasu na maturze Ci zabraknie  MOżna prościej
|AS|=...
sinα=...
MOżna prościej
|AS|=...
sinα=...
 Pokaż, że te trójkąty ABS i ACS są przystające.
Pokaż, że te trójkąty ABS i ACS są przystające.
 już jasne
już jasne 


 coś w tym jest
coś w tym jest  r=√5
r2+x2=|AS|2
|AS|2=(−1−2)2+12=10
|AS|=√10
5+x2=10
x2=5
x=√5
(nie wiem w sumie po co to wyliczyłem, ale niech już zostanie)
r=√5
r2+x2=|AS|2
|AS|2=(−1−2)2+12=10
|AS|=√10
5+x2=10
x2=5
x=√5
(nie wiem w sumie po co to wyliczyłem, ale niech już zostanie)


 jutro można coś się na discordzie złapać i porobić
jutro można coś się na discordzie złapać i porobić



 jeszcze należy pokazać, że trójmian kwadratowy nie ma pierwiastków naturalnych.
jeszcze należy pokazać, że trójmian kwadratowy nie ma pierwiastków naturalnych.