Okręgi styczne zewnętrznie wpisane w półkole Agnieszka : Dwa okręgi o promieniu r są styczne zewnętrznie i wpisane w półkole o promieniu 1. Oblicz r

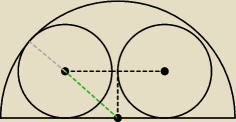
wredulus_pospolitus: To tak samo jakbyś miał/−a jeden okrąg wpisany w ćwiartkę okręgu o promieniu 1. Jak wyznaczyć długość zielonego odcinka

xxx: Za duża "luka " między nimi

Agnieszka : Czy jest ktoś w stanie pomóc?

ford: w trójkącie prostokątnym widocznym na rysunku z godz. 18:31 pionowy przerywany odcinek ma długość r (bo jest równy długości promienia każdego z dwóch mniejszych kółek) zielony odcinek jest różnicą promienia półkola (1) i małego kółka (r) więc zielony = 1 − r r² + r² = (1−r)² 2r² = 1−2r+r² r²+2r−1 = 0 Δ=8 √Δ = 2√2 r₁ = U{−2−2√2{2} = −1−√2 odpada r₂ = U{−2+2√2{2} = √2−1

Agnieszka : Wyszło mi że zielony odcinek to 1−r, lecz nie mam pewności czy dobrze, ale co dalej?

Agnieszka : Przepraszam, nie widziałam odpowiedzi

Agnieszka : A czy da się to obliczyć jakoś inaczej niż na deltę, ponieważ jeszcze tego nie mieliśmy

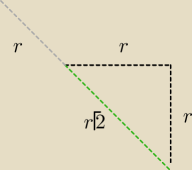
a7: r+r√2=1 r(1+√2)=1 r=U{1]{1+√2}=√2−1

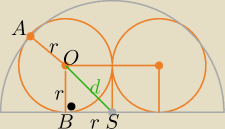
Stefcia: d= |AS|−|AO|= 1−r i d=r√2 długość przekątnej kwadratu o boku r to r√2=1−r r(√2+1)=1 /*(√2−1) r(2−1)=√2−1 r=√2−1 ========

ford: z własności trójkąta o kątach 90⁰, 45⁰, 45⁰ (ma boki r, r, r*√2 − oczywiście zielony to r*√2 ponieważ najdłuższy (czyli zielony) to również 1−r więc r*√2 = 1−r r*√2 + r = 1 r(√2 + 1) = 1

	1
r =
	√2+1

po usunięciu niewymierności z mianownika wyjdzie że r = √2−1

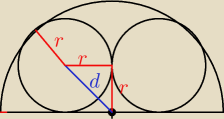
Saizou : d=r√2 (z Pitagorasa) r√2+r=1 r(√2+1)=1

	1
r=		=√2−1
	√2+1

Stefcia:

Saizou :

Stefcia:

Saizou : Znowu się ukrywasz?

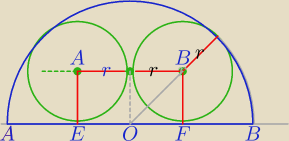
Mila: |OB|+r=1 r√2+r=1 r*(√2+1)=1 /*(√2−1) r*(2−1)=√2−1 r=√2−1

Stefcia: Spóźniony "zapłon"

Mila: Ale się spóźniłam

Mila: Rudecka działa jak błyskawica

Stefcia: