Półokrąg wpisany w trójkąt równoramienny
Agnieszka : Dany jest trójkąt równoramienny ABC, w którym podstawa AB ma długość 17,6 cm, a ramiona AC i BC
są równe 18,7 cm. W trójkąt ten wpisano półokrąg o środku O, styczny do boków AB i BC. Znajdź
długość promieni wpisanego półokręgu.
30 mar 17:48
Agnieszka:
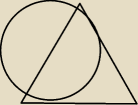
Tutaj jest rysunek, tylko że na nim ma byc samo półkole wpisane w trójkąt (bez tej drugiej
części koła)
30 mar 18:42
Mila:
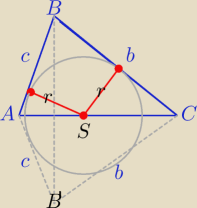
P
ABCC'=2*P
ΔABC
Licz
30 mar 18:52
Agnieszka : Mogłabyś mi wytłumaczyć co to za figura ABCC'? Bo nie mogę się za bardzo połapać
30 mar 18:54
Mila:
Przepraszam, źle tam napisałam− nieuważnie naciskałam klawisze.
Odbicie symetryczne ΔACB względem prostej AC, powstał deltoid, ABCB'.
30 mar 19:16
Agnieszka : Rozumiem, a jakbys mogła mi jeszcze wytłumaczyć skąd wzór na 2*PΔABC to 2b+2c/2*r?
30 mar 19:21
30 mar 19:24
Agnieszka : A no tak, już rozumiem.. dzięki serdeczne ❤️
30 mar 19:26
Shizzer:
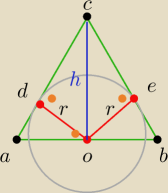
Można byłoby podejść do tego tak?
|AO|= 17,6/2 = 8,8
h
2 + (8,8)
2 = (18,7)
2
h
2 = 272,25
h = 16,5
Z podobieństwa trójkątów:
ΔDOC ~ΔOAC na podstawie cechy KKK więc
|AC|h =
|AO|r
18,716,5 =
8,8r
18,7r = 145,2 /:18,7
Ale z tego wychodzi jakiś straszny ułamek. Dobre jest to rozwiązanie czy gdzieś źle coś
zrobiłem?
30 mar 19:29
Agnieszka : Półokrąg miał być styczny do boku AB i BC, a na twoim rysunku jest styczny do AC i BC
30 mar 19:33
Shizzer: No tak! Dzięki za zwrócenie uwagi
30 mar 19:37
Agnieszka : Miła a czy mogłabyś podać ile powinien wynosić promień, gdyż nie jestem pewna czy dobrze mi
wyszło
30 mar 20:04
Mila:
Zaraz policzę.
30 mar 20:06
Mila:
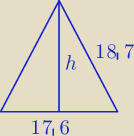
h
2=18,7
2−8.8
2
h
2=272,25
h=16.5
2P
ABC=17.7*16.5=290.4
290.4=(b+c)*r
290.4=(18,7+17.6)*r
r=U{290.4}{36.3)
r=8
===
30 mar 20:17
30 mar 20:18
Agnieszka : Dziękuję bardzo jeszcze raz, również mi tyle wyszło
30 mar 20:18
Mila:
Strasznie to wyglądało, ale ładnie się policzyło.
30 mar 20:20
 Tutaj jest rysunek, tylko że na nim ma byc samo półkole wpisane w trójkąt (bez tej drugiej
części koła)
Tutaj jest rysunek, tylko że na nim ma byc samo półkole wpisane w trójkąt (bez tej drugiej
części koła)
 PABCC'=2*PΔABC
PABCC'=2*PΔABC
 Można byłoby podejść do tego tak?
|AO|= 17,6/2 = 8,8
h2 + (8,8)2 = (18,7)2
h2 = 272,25
h = 16,5
Z podobieństwa trójkątów:
ΔDOC ~ΔOAC na podstawie cechy KKK więc
|AC|h = |AO|r
18,716,5 = 8,8r
18,7r = 145,2 /:18,7
Ale z tego wychodzi jakiś straszny ułamek. Dobre jest to rozwiązanie czy gdzieś źle coś
zrobiłem?
Można byłoby podejść do tego tak?
|AO|= 17,6/2 = 8,8
h2 + (8,8)2 = (18,7)2
h2 = 272,25
h = 16,5
Z podobieństwa trójkątów:
ΔDOC ~ΔOAC na podstawie cechy KKK więc
|AC|h = |AO|r
18,716,5 = 8,8r
18,7r = 145,2 /:18,7
Ale z tego wychodzi jakiś straszny ułamek. Dobre jest to rozwiązanie czy gdzieś źle coś
zrobiłem?
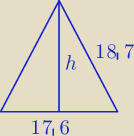 h2=18,72−8.82
h2=272,25
h=16.5
2PABC=17.7*16.5=290.4
290.4=(b+c)*r
290.4=(18,7+17.6)*r
r=U{290.4}{36.3)
r=8
===
h2=18,72−8.82
h2=272,25
h=16.5
2PABC=17.7*16.5=290.4
290.4=(b+c)*r
290.4=(18,7+17.6)*r
r=U{290.4}{36.3)
r=8
===