Znajdź równanie tej stycznej do wykresu funkcji x^3-2, która przechodzi przez po czarniecki: Znajdź równanie tej stycznej do wykresu funkcji x³−2, która przechodzi przez początek układu współrzędnych. Policzyłem f`(x)=3x<sup>2</sup>, następnie do wzoru y=f`(x0)(x−x0)+f(x0) podstawiłem punkt 0,0 i dostałem równanie: −2x0²=2, a więc x0=−1 z tego f`(x0)=3, a f(x0)=−3 i z tego równanie tej stycznej y=3x, ale gdzieś musi być błąd, bo źle wychodzi.

piotr: nie jest powiedziane, że punkt (0,0) to punkt styczności

Jerzy: y = f'(0)( x − 0) + f(0) y = 0(x − 0) + 2 = 2 y = 2

Jerzy: y = −2

Jerzy: Bzdura

czarniecki: Czemu pod x0 podstawiłeś 0, skoro to nie jest punkt styczności?

daras: https://matematykaszkolna.pl/strona/379.html

Des: P=(0,0) ,P∉f(x) y=ax+b −−−−−−−−−− 0=0a+b b=0

	f(x0) − 0
f '(x0)=
	x0 − 0

f'(x₀)x₀=f(x₀) ⇒ x₀= ⇒ f(x₀) =

	f(x0)
a=		=
	x0

czarniecki: @daras tam jest w punkcie, a u mnie jest "która przechodzi przez punkt", czyli ten punkt to nie jest punkt styczności

czarniecki: Może mi ktoś wytłumaczyć, co jest złego w moim rozumowaniu?

Des: y=3x to prawidłowy wynik

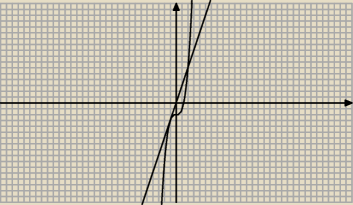
czarniecki: No ale to jest przecinane w dwóch miejscach, więc co to za styczna

Jerzy: Styczna może przecinać wykres funkcji w innych pynktach.

czarniecki: Ah, ok. Dzięki wielkie