stereo dowód
jaros: Ostrosłup prawidłowy czworokątny przecięto płaszczyzną prostopadłą do jednej z krawędzi
bocznych ostrosłupa i jednocześnie zawierającą przekątną podstawy. Otrzymany przekrój jest
trójkątem rozwartokątnym którego kąt rozwarty ma miarę 2α. Wyznacz cos kąta β nachylenia
płaszczyzny tego przekroju do płaszczyzny podstawy.
Proszę o pomoc nie wiem jak to dowieść lecz rysunek mam.
30 mar 14:48
jaros:
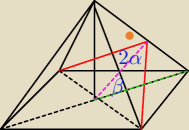
30 mar 14:50
tania: Wprowadz a −krawedz podsatwy
Nie znaczyłes tam waznego odcinka bo Pitagorasa możesz go policzyć :cześć krawdzedzi bocznej
od podstawy.
30 mar 14:59
jaros: | | a√2 | |
No rozumiem, że połowa przekątnej to |
| ale co z tym zrobić? |
| | 2 | |
30 mar 15:01
salamandra: już ci piszę, daj mi chwilę
30 mar 15:04
salamandra:
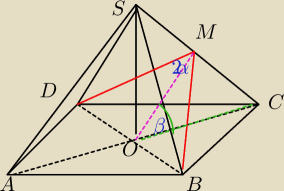
DB=a
√2
OM=h
w ΔOMB
W ΔOMC
30 mar 15:09
30 mar 15:10
Saizou :
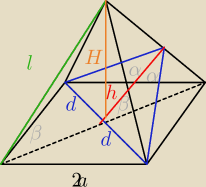
d=a
√2
l=2h
30 mar 15:12
jaros: Okej, wszystko rozumiem, Dziękuję ślicznie @salamandra jak i @Saizou
30 mar 15:22

 DB=a√2
OM=h
DB=a√2
OM=h
 d=a√2
d=a√2