zadanie z arkusza maturalnego - poziom rozszerzony
3003:
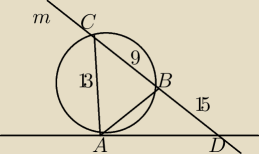
Na poniższym rysunku przedstawiono okrąg opisany na trójkącie ABC oraz styczną do tego okręgu
w punkcie A. Ponadto dany okrąg przecina prosta m oraz dane są długości odcinków |AC|=13,
|BC|=9, |BD|=9. Znajdź długość odcinka AB. Wynik zaokrąglij do jedności.
30 mar 11:33
f123: Wylicz dlugosc odcinka |AD| (z pitagorasa) a nastepnie pole trojkata ADC, i przyrownaj do wzoru
na pole z sinα − wylicz sinα (kat ACD) a nastepnie cosα i pozniej z tw cosinusow obliczysz
|AB|
30 mar 11:38
3003: f123 − na jakiej podstawie zakładasz, że odcinki AD i AC są prostopadłe?
30 mar 11:42
f123: Styczna w punkcie A − cos ci to mowi?
30 mar 11:43
3003: f123 − no tak, w takim razie dzięki za pomoc!
30 mar 11:44
3003: f123 − słuchaj, ale z jakiej zasady stwierdzasz, że ten AC jest prostopadły do AD? bo ja
rozumiem,
że w punkcie A jest styczna, ale jak tą prostą przechylisz w dół to nadal będzie styczną, a AC
nie
będzie prostopadłe do niej. teraz też nie mamy na jakiej podstawie stwierdzić, że tam
faktycznie jest
kąt prosty. liczę na jakieś wytłumaczenie, może to jest moje niedpoatrzenie
30 mar 12:13
f123: @3003 fakt, nie wiemy tego, to w takim razie odcinek |AD| obliczasz z twierdzenia o odcinkach
stycznych, a nastepnie pole ze wzoru herona i dalej postepujesz tak samo
30 mar 12:16
f123: |CD| * |BD| = |AD|2
30 mar 12:16
3003: f123 − dzięki
30 mar 12:20
3003: f123 − właściwie to nie, nie rozumiem. policzyłam z wzoru herona pole trójkąta, obliczyłam
sinus kąta ACD, wychodzą mi liczby z kosmosu, a rozwiązanie nadal daleko. co mam zrobić mając
wyliczony ten sinus? skąd wziąć cosinus? pozdrawiam i życzę miłego dnia
30 mar 13:00
f123: nastepnie liczysz cosα z jedynki trygonometrycznej, a pozniej w trojkacie ABC tw cos
|AB|2 = 92 + 132 − 2 * 9 * 13 * cosα
30 mar 13:03
3003: f123 − wychodzą naprawdę niesamowite liczby, przeanalizuję wszystko jeszcze raz i zobaczymy
30 mar 13:09
f123: a jaka ci dlugosc odcinak |AB| wyszla?
30 mar 13:11
3003: √(151715+44280√10)/1664
30 mar 13:17
f123: to cos nie tak, zaraz postaram sie znalezl inny sposob
30 mar 13:21
f123: A miary katow ADB i ABC nie sa takie same? Katy oparte na tym samym luku
30 mar 13:22
f123: Nie jednak nie
30 mar 13:23
Już za miesiąc: Rozwiązał ktoś to do końca ?
24 kwi 12:25
ICSP: AB = x
|AD|
2 = |BD|*|CD|
|AD| = 6
√6
∡ABD = α
z twierdzenia cosinusów dla ΔABD:
216 = x
2 + 15
2 − 30xcosα
z twierdzenia cosinusów dla ΔABC:
169 = x
2 + 81 + 18xcosα
216 = x
2 + 15
2 − 30xcosα
169 = x
2 + 81 + 18xcosα
−9 = x
2 − 30xcosα // *3
88 = x
2 + 18xcosα // * 5
−27 = 3x
2 − 90xcosα
440 = 5x
2 + 90xcosα
−−−−−−−−−−−−−−−−−−−−−−−−
413 = 8x
2
24 kwi 12:44
mat:
|AD|= 6√6 ? ?
24 kwi 15:11
Louie314: Z twierdzenia o odcinkach siecznej i stycznej można policzyć |AD|:
|CD|*|BD|=|AD|2
24*15=|AD|2
360=|AD|2
|AD|=6√10
24 kwi 15:22
 Na poniższym rysunku przedstawiono okrąg opisany na trójkącie ABC oraz styczną do tego okręgu
w punkcie A. Ponadto dany okrąg przecina prosta m oraz dane są długości odcinków |AC|=13,
|BC|=9, |BD|=9. Znajdź długość odcinka AB. Wynik zaokrąglij do jedności.
Na poniższym rysunku przedstawiono okrąg opisany na trójkącie ABC oraz styczną do tego okręgu
w punkcie A. Ponadto dany okrąg przecina prosta m oraz dane są długości odcinków |AC|=13,
|BC|=9, |BD|=9. Znajdź długość odcinka AB. Wynik zaokrąglij do jedności.