Trapez równoramienny Klara : Odcinek łączący środki ramion trapezu równoramienny go na długość 5 i dzieli go na dwie figury, których pola mają się do siebie, jak 7:13. Wiadomo też, że w dany trapez można wpisać okrąg. Oblicz długość wysokości trapezu

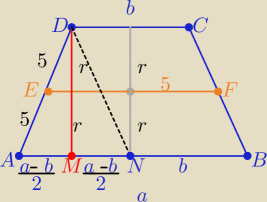
Eta: Z treści zadania :

	P(EFCD)		7
h=2r i		=		i a+b=2c
	P(ABFE)		13

	a+b
|EF| =		=5 ⇒ a+b=10 to a= 10−b , b∊(0,10)
	2

5+b		7
	=		⇒ 65+13b=35+7a ⇒ 7a−13b= 30 i a=10−b
5+a		13

	a−b
to ... b= 2 więc a= 8 i		= 3
	2

z tw. Pitagorasa w ΔAMD 2r=h= 4 ========

Klara: Mogłabyś wyjaśnić dlaczego EF = a+b/2?

Klara: Oraz dlaczego AE i ED mają po 5?

f123:

	a + b
|EF| jest to odcinek laczacy srodki ramion trapezu, wzor na |EF| =
	2

Klara : A EE i ED Dlaczego mają po 5?

Klara : Nie powinno być ze całość AD to 5?

janek191: ? a + b = 10 ale 2 c = 20 ? Powinno być: I AE I = I ED I = 2,5

Eta: |AD|=5 ( na rysunku pomyłkowo nie wpisałam 2,5 i 2,5 ale już w Pitagorasie wpisałam dobrze h²= 5²−3² ⇒h=4