Bryły Gangster: Odległośc srodka podstawy ostroslupa prawidlowego czworokatnego od sciany bocznej jest rowna d, a kąt sciany bocznej przy wierzchołku ostrosłupa ma miarę α. Oblicz V ostrosłupa. Strasznie męcze te zadania zajmuja mi one baaaardzo dużo czasu, i nie da sie ukryć ze sa dosc skomplikowane, jest szansa ze takie pojawia sie na maturze? Czy to gra nie warta swieczki i skupic sa na innych zadaniach?

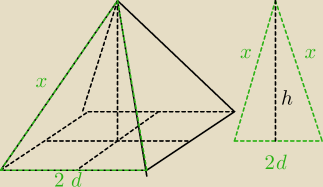
wredulus_pospolitus: wyznaczasz 'h_{ściany bocznej}' zależne od 'd' i kąta (α/2) Budujesz kolejny trójkąt prostokątny w celu wyznaczeni H_ostrosłupa mając h_{ściany bocznej} i d Wstawiasz do wzoru na objętość

wredulus_pospolitus: Planimetrię / geometrię na 100% będziesz miał na maturze i to parę zadań (w tym jakieś otwarte), jeżeli celujesz w 80+ to jest to 'must be'.

Gangster: Mniej wiecej wiem o co w tym chodzi, ale czy jest sens teraz sie nad tym meczyc? bo sa bardzo czasochlonne i sie mocno denerwuje a na starych arkuszach nic podobnego nie widzialem

f123: Oczywiscie ze beda, ale zalezy jak trafimy. Mam nadzieje ze zadania z planimetrii / stereometrii beda z wartosciami liczbowymi.

f123: Zadania ze stereometri sa wysoko punktowane (5 / 6 pkt)

Saizou : Ostatnio jest trend aby te zadania ze stereometrii łączyły w sobie optymalizację

Gangster: oczyiwscie ze beda, jednak mi chodzi o to czy AZ tak skomplikowane? bo z tego co patrze to na maturze zdarzaja sie wlasnie tak jak mowisz z wartosciami liczbowymi ewentualnie wykazac cos na trojkatach a to zadanie w odpowiedziach zajmuje pol strony.

f123: Niestety nie wiadomo, trzeba liczyc na to aby byly z wartosciami liczboywmi, albo na to ze napiszemy mature w czerwcu / lipcu

Saizou : Trzeba liczyć na siebie i swoje umiejętności Maturzyści

salamandra: Według mnie optymalizacja ze stereometrii to jedna z przyjazniejszych rzeczy jakie mogą się trafić na maturze

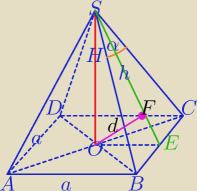
Mila: 1) W ΔSEC:

	α		0.5a		a
tg		=		⇔h=
	2		h		α   2tg   2

2) W ΔSOE: OE⊥SE

1		a		1
	*		*H=		h*d
2		2		2

a		a		d
	*H=		*d ⇔H=
2		α   2tg   2		α   tg   2

3)

	a		d		a2		a
H2+(		)2=h2 ⇔(		)2+		=(		)2
	2		α   tg   2		4		α   2tg   2

d2		a2		1
	=		*(		−1)
α   tg2   2		4		α   tg2   2

d2		a2		α   1−tg2   2
	=		*
α   tg2   2		4		α   tg2   2

	4d2
a2=
	α   1−tg2   2

	1		4d2		d
V=		*		*
	3		α   1−tg2   2		α   tg   2

	4d3
V=
	α   α   3tg *(1−tg2 )   2   2

============================