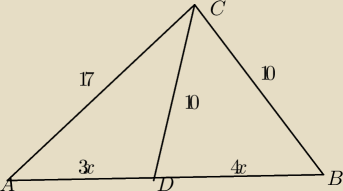
planimetria salamandra: Dany jest trójkąt ABC w którym AC=17 i BC=10. Na boku AB leży taki punkt D, że ADB=3:4 oraz DC=10. Oblicz pole trójkąta ABC w ΔABC z tw cosinusów: 10²=289+49x²−34*7x*cosα −189=49x²−238x*cosα w ΔADC 100=289+9x²−102x*cosα −189=9x²−102x*cosα

⎧	−189=49x2−238x*cosα
⎩	−189=9x2−102x*cosα

teraz nie wiem jak ugryźć ten układ równań metodą przeciwnych współczynników, nie widzę co przez ile przemnożyć. Jest jakiś sposób, żeby to szybko znaleźć? Pewnie jak posiedzę trochę z kalkulatorem to w końcu znajdę. A może mam błąd?

salamandra: znalazłem, *6 i *14

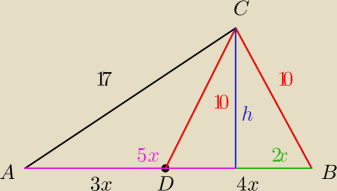
Saizou : 2x Pitagoras

Gangster: skorzystaj z tw o dwusiecznej a pozniej z wzoru herona, mysle ze bedzie duzo prosciej i szybciej

salamandra: a gdzie ja tu mam dwusieczną?

Gangster: aj, rzeczywiscie nie ma akurat, przed chwila robilem podobnie zadanie gdzie byla dwusieczna i jakos uznalem ze tutaj tez jest, przepraszam. w tkaim raziem pomysl saizou bedzie najlepszy

salamandra: dokończę swoim jak już znalazłem te wspolna wielokrotnosc, ale faktycznie, tam mam trojkat rownoramienny w rozwiazaniu Saizou i też ładnie wyjdzie

Gangster: salamandra, na jakie studia sie wybierasz?

salamandra: planuje na PG na informatyke

salamandra:

⎧	1134=−294x2+1428x*cosα
⎩	−2646=126x2−1428x*cosα

−1512=−168x² x²=9 ⇒ x=3 podstawiam do pierwszego, aby obliczyć cos, a następnie sin i zastosować wzór na pole

	1
		absinα
	2

−189=81−306*cosα −270=−306*cosα

270
	=cosα
306

	15
cosα=
	17

225
	+sin2α=1
289

64
	=sin2α
289

	8
sinα=		, bo α ostry.
	17

	1		8
P=		*17*21*		=84
	2		17

Saizou : Wynik jest okej, ale droga na około

salamandra: przyznam, że zadanie wcześniej było analogiczne (co wstawiałem na forum) i z automatu tutaj miałem taki odruch, żeby w ten sam sposób zrobić to zadanie z matury 2013 rozszerzonej za 5 pkt aż, przyjemne

Saizou : bardzo proste jak na rozszerzenie

salamandra: i to stare rozszerzenie, rzekomo trudniejsze

Gangster: mam wrazenie ze na tych starszych maturach trafialy sie albo sporo trudniejsze albo sporo latwiejsze zadania

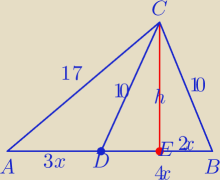
Mila: 1) W ΔAEC i w ΔCEB: h²+(5x)²=17² h²+(2x)²=10² ========== odejmuję stronami 21x²=189 x²=9 x=3 2) AB|=7*3=21

	17+21+10
p=		=24
	2

3) P_ΔABC=√24*(24−17)*(24−10)*(24−21)=√24*7*14*3=√8*3*7²*2*3 P_ΔABC=4*3*7=84

Mila: lub 2) w ΔCEB: 2x=6 h²=100−36 h=8

	1
3) PΔ=		*21*6=84
	2

an: dobrze że macie kalkulatory, bo kiedyś to się tak liczyło 238/7=34 i 102/3=34

salamandra: dzięki za alternatywę