maraton Saizou : maraton #2 2a) Rozwiąż nierówność tg 2x < 2sinx w przedziale x∊(0, π) oraz 2b) Rozwiąż nierówność tg x + ctgx < 4sin2x x∊(0, 2π)

Szkolniak: ad 2a

2sinxcosx		k
	<2sinx ∧ (cos2x≠0 ⇔ x≠		π)
2cos2x−1		4

cosx
	<1, bo dla x∊(0;90o) 2sinx>0
2cos2x−1

cosx−2cos2x+1
	<0
2cos2x−1

cosx=t

t−2t2+1
	<0
2t2−1

(−2t²+t+1)(2t²−1)<0

	1
−2(2t2−t−1)(t2−		)<0
	2

	1		√2		√2
(t+		)(t−1)(t+		)(t−		)>0
	2		2		2

	√2		1		√2
cosx∊<−1;−		)∪(−		;		) ∧ x∊(0;π)
	2		2		2

	π		π		π		π		π		2		5
Odpowiedź: x∊(		;		)∪(		;		)∪(		;		π)∪(		π;π)
	6		4		4		2		2		3		6

I jak? Odpowiedź dobra?

f123: To ja cos podrzuce: sinx + cosx = 3, x ∊ <0, 2π>

Szkolniak: x∊∅

f123: @szkolniak

Saizou : Szkolniak sprawdź raz jeszcze odpowiedź, bo do momentu cosx∊ jest okej. x∊∅ (to zbiór jest pusty czy ma w sobie x)

Szkolniak: W sensie? 'x' należy do zbioru pustego (nie istnieje taki iks, który spełniałby podane równanie) Włącznie z cosx∊ jest okej?

Saizou : Tak, błędna jest odpowiedź.

	√3
Cos(pi/6)=
	2

Wiec coś jest nie halo

Szkolniak: tfu.. pomyliłem z sinusem

	π		π		π		2		5
x∊(		;		)∪(		;		π)∪(		π;π)
	3		2		2		3		6

teraz?

Saizou :

	π
x1=
	4

	4		2
x2=		π=		π
	6		3

	3
x3=		π
	4

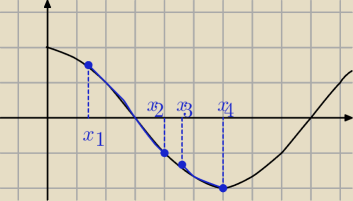
x₄=π +założenie

Szkolniak: Ale namieszałem z tymi wartościami.. już rozumiem

Saizou : na przyszłość trzeba dobry wykres narysować

Szkolniak: Narysowany dobry, ale w głowie już wszystkie wartości przelatywały − tyle założeń, podstawienia, odczytywanie z wykresu

Saizou : b) jest podobne

Szkolniak: ad 2b x∊(0;2π)

sinx		cosx
	+		<4sin2x, cosx≠0 ∧ sinx≠0
cosx		sinx

1
	<8sinxcosx
sinxcosx

2
	<4sin2x
sin2x

1
	<sin2x
2sin2x

Teraz najlepiej podstawienie t=sin2x?

Saizou : Tak

Szkolniak:

1
	<t /*2t2
2t

t<2t³ 2t³−t>0 t(2t²−1)>0

	√2		√2
t(t+		)(t−		)>0 ∧ t∊<−1;1>
	2		2

	√2		√2
t∊(−		;0)∪(		;1>
	2		2

	√2		√2
zatem: sin(2x)∊(−		;0)∪(		;1>
	2		2

Mogę to teraz w jakiś sprytny sposób zrobić? Czy muszę to narysować i odczytywać z wykresu funkcji wszystko?

Saizou : popraw rozwiązanie t∊....

	π
i najlepiej narysować sin(2x) (tip: tak nietypowo można zaznaczyć		, co 6 kratek)
	2

Szkolniak: nie widzę.. co jest nie tak w t∊...?

Saizou : a nie, jest okej, ja u siebie rozwiązywałem wersję z nierównością w drugą stronę

Szkolniak:

	π		π		2		π		5		7		5
odpowiedź: x∊(		;		)∪(		π;		)∪(		π;π)∪(		π;		π)∪
	6		4		3		2		6		6		4

	3		5		11
∪(		π;		π)∪(		π;2π)
	2		3		6

tak o? + założenia, że cosx≠0 i sinx≠0

Saizou : podstaw sobie 2x=p i wówczas sin p ∊... wychodzi jakieś rozwiązanie ogólne i x∊... bo znowu się gubisz

Szkolniak: dobra, czyli robimy podstawienie 2x=p, wtedy: 1) sin(p)∊... i z tego odczytuje, że p∊... 2) wtedy 2x∊.... i wystarczy 'podzielić' przez dwa i wychodzi, że x∊... dobrze rozumiem?

Saizou : Tak

Szkolniak: a sin(p)∊... wyznaczam tylko w przedziale (0;2π), tak?

Saizou : Nie, bo wtedy jak podzielisz na 2 to przedział się skurczy.

f123: x ∊ <0, 2π> 2x ∊ <0, 4π>

Saizou : tutaj masz rysunek https://www.geogebra.org/graphing/k5phhnzv

	π
jednostka na osi x to
	8

Szkolniak: Czyli jak rozpatruje powiedzmy sin(5x) to muszę odczytać z przedziału <0;10π> żeby potem, dzieląc przez 5, wyszedł mi przedział z zadania, czyli <0;2π>? A co do linku to niestety wyskakuje mi błąd

Saizou : to masz tutaj https://drive.google.com/file/d/1ruTyV9im_W__d_t3bIVMuyuKNVWtuJVW/view?usp=sharing tak, ale w takich przypadkach lepiej rozwiązać ogólnie i potem wybrać odpowiednie rozwiązania.