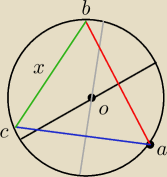
Długość odcinka xoxo: Z dowolnego punktu na okręgu opuszczono proste prostopadłe na dwie ustalone średnice tego okręgu. Pokaż, że długość odcinka łączącego spodki tych prostopadłych nie zależy od wyboru punktu na okręgu. Zauważyłam, że przyjmując, że kąt CAB=α i kąt środkowy COB=2α można skorzystać z tw cosinusów i wyznaczyć wartość x, zależnego tylko od promienia i kąta, jednak w tym zadaniu nie mogę skorzystać z tego twierdzenia Jakiś pomysł lub wskazówka jak można to pokazać inaczej?

wredulus_pospolitus: Co oznacza, że 'nie możesz skorzystać z tego twierdzenia' Bo jest odgórnie zakazane, czy według Ciebie nie można z niego skorzystać

f123: Hmm, te trojkaty beda przystajace (cecha (bkb)

wredulus_pospolitus: tw. sinusów Czy też z tego co 'niby nie możesz' czy to z tw. sinusów −−− kluczem do zadania jest pokazanie, że ∡CAB = α = const.

wredulus_pospolitus: f123 −−− nie ... nie będą chyba że chcesz mi powiedzieć, że te da trójkąty są przystające ... to będę wielce rad za pokazanie dowodu

f123: @wredulus_pospolitus analizowalem nie te trojkaty, chyba czas isc spac...

salamandra: jakie spać, o tej godzinie się najlepiej pracuje!

f123: @salamandra wlasnie sie dowiedzialem, ze moja szkola bierze udzial w maturze probnej od cke przez internet, ciekawe jak to bedzie wygladac...

xoxo: Odgórnie nie możemy koszystać z bardziej "zaawansowanych" twierdzień i wymagany jest dowód na podstawie elementarnych rzeczy np. trójkąty podobne, kąty wpisane itp

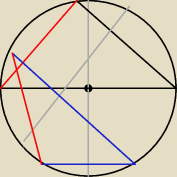
wredulus_pospolitus: Co prawda ja nie narysowałem dwóch średni ... ale tą jedną cięciwę można po prostu przesunąć równolegle, aby była średnicą −−− same trójkąty nie ulegną zmianie krok 1: wiemy, że średnice przecinają się pod KONKRETNYM kątem, zaznaczamy go. krok 2: budujemy czworokąt: Środek okręgu, punkty przecięcia się średnic z bokami, wierzchołek A krok 3: wyznaczamy ile jest równy kąt przy wierzchołku A krok 4: stosujemy tw. sinusów I po ptokach.

wredulus_pospolitus: No to jaka jest lista tych nie 'bardziej zaawansowanych' twierdzeń To jest wymóg nauczyciela

xoxo: To zadanie jest z listy w której mamy wykorzystać tw związane z kątami wpisanymi, kątem środkowym i trójkątami podobnymi. Tak to wymóg nauczyciela. Tylko, że ja nie widzę tu innego rozwiązania niż skorzystanie z tw sin lub cos