pochodna, zadanie optymalizacyjne PilnyUczen: Mam pytanie czy w tym zadaniu mogę skorzystać ze wzoru na pochodna złożona? 1.Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie 20. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.

wredulus_pospolitus: A jaką postać funkcji objętości stworzyliśmy

salamandra: L=20 2l+2r=20 l+r=10 l=10−r H²+r²=(10−r)² H²+r²=100−20r+r² H²=100−20r H=√100−20r

	1		1
V=		*Pp*H=		*πr2*√100−20r
	3		3

f(r)=r²*√100−20r= √100r⁴−20r⁵ omijamy pierwiastek −20r⁵+100r⁴=g(r) g'(r)=−100r⁴+400r³ −100r⁴+400x³=0 −100r³(r−4)=0 r=0 v r=4 max dla r=4 wtedy H=√100−80=√20=2√5 nie jestem pewien, więc niech ktoś potwierdzi/poprawi

f123: Mozesz, ale pytanie po co?

salamandra:

	1		32√5
A, no i objetosc to oczywiście V=		*π*16*2√5=		, ale tak jak mówię, nie jestem
	3		3

pewien, więc ktoś sprawdzi najwyżej

xyz: korzystaj, jesli umiesz ja wyliczyc, to jak najbardziej popieram. Przy podstawianiu nowej funkcji np. jak mamy f(x) = √x²+4x+1 i robimy g(x) = x²+4+1 to wypada wg mnie dopisac cos w stylu "Funkcja g(x) osiaga ekstrema dla tych samych argumentow co funkcja f(x), jedynie wartosci tych ekstremow beda inne".

f123: @xyz oczywiscie, komentarz na maturze jak najbardziej wskazany

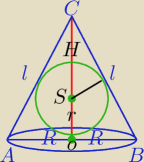
Mila: Nie wiem, czy mniej liczenia, ale można uzależnić V od H 2l+2r=20 l+R=10 l²=H²+R² (10−R)²=H²+R² 100−20R+R²=H²+R² 100−20R=H² 100−H²=20R

	100−H2
R=		i 0<H<10
	20

	1		π		100−H2
V(H)=		π*R2*H=		*(		)2*H
	3		3		20

spróbuj tak dokończyć, będzie bez pierwiastka.

salamandra: też nad tym właśnie myślałem, ale juz mi sie nie chciało zmieniać, mam nadzieję, że wyszlo dobrze