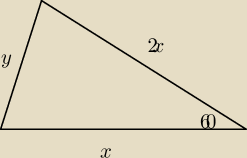
planimetria salamandra: Jeden z kątów trójkąta o obwodzie 6 ma miarę 60, a stosunek dlugosci boków zawartych w ramionach tego kąta jest równy 1:2. Oblicz pole trójkąta. 3x+y=6 y=6−3x z tw. cosinusów: (6−3x)²=x²+4x²−4x²*cos60 36−36x+9x²=5x²−2x² 6x²−36x+36=0 Δ=12 √Δ=2√3

	6−2√3
x1=		=3−√3
	2

x2=3+√3 i teraz nie wiem który "x" mam wziąć pod uwagę w liczeniu pola. Odpowiedź to: 3(2√3−3)

	1
P=		*(3+√3)*(6+2√3)*sin60=6√3+9=3(3+2√3) dla x=3+√3
	2

	1
dla x=3−√3 = P=		*(3−√3)*(6−2√3)*sin60= 3(2√3−3)
	2

dlaczego jeden x odpada, skoro nierówność trójkąta jest spełniona dla obu pierwiastków równania?

salamandra: a nie, nieistotne, dla 3+√3 y=6−3*(3+√3)=6−9−3√3=−3−3√3=−3(1+√3) < 0

f123: @salamandra dokladnie, zalozenia

salamandra: za pierwszym razem jak sprawdzałem to miałem na plusie, nie wiem co nie tak zrobiłem,