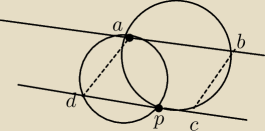
Udowodnij, że ABCD jest równoległobokiem Elena: Okręg s1 i s2 przecinają się w punktach A i P. Prosta AB jest styczna do s1 w A, a prosta CD jest równoległa do AB i przechodzi przez punkt P, przy czym punkty B i C leżą na okręgu s2, a punkt D na okręgu s1. Udowodnij, że ABCD jest równoległobokiem. (wiem, że rysunek nie jest dokładny) Niestety nie mam pomysłu na to zadanie Jakaś wskazówka jak można to udowodnić?

ite: Najpierw pokaż, że APCB jest trapezem równoramiennym czyli kąty przy dłuższej podstawie ma równe. Potem wykaż, że również <PAB i <PDA są równe.

Elena: Czy na to, że APCB jest trapezem równoramiennym wystarczy wskazać, że kąt DPA= PAB (bo są naprzeciwległe) oraz z własności czworokąta wpisanego w okrąg, suma jego przeciwległych kątów jest równa 180?

ite: W okrąg można wpisać trapez jedynie równoramienny. Więc jeśli wiemy, że czworokąt można wpisać w okrąg i jest trapezem, to jest to trapez równoramienny. Stąd miary kątów przy dłuższej podstawie są równe. Pozostaje jeszcze pokazać, że miary <PAB i <PDA są równe. Rysunek jest niedokładny, a to nie pomaga.

Elena: Narysowałam dokładniejszy rysunek, na innej stronie, i wynika, że będzie to trójkąt równoboczny. W trójkącie APD wynika, że kąt DPA= α tak jak kąty PAB i CBA. Jednak nie mam pomysłu jak udowodnić, że dwa pozostałe kąty w trójkącie też są równe α

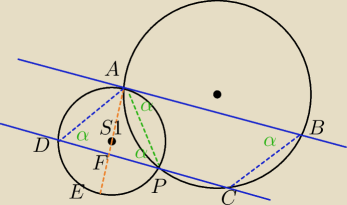
ite: AS promień okregu O₁ DP cięciwa okręgu AS₁⊥AB AB ||DC AF⊥DP |DF|=|FP| ΔADF≡ΔAFP → |<ADP|=|<DPA| ΔADP równoramienny

Elena: Dziękuje!