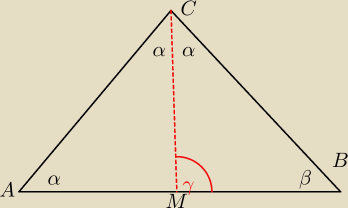
planimetria salamandra: W trójkącie ABC miara kąta ACB jest dwa razy większa od miary kąta CAB. Dwusieczna kąta ACB dzieli trójkąt ABC na dwa trójkąty. Uzasadnij, że co najmniej jeden z otrzymanych trójkątów: a) jest równoramienny, b) jest podobny do trójkąta ABC. a) |AM|=|CM|, bo kąty przy podstawie są równe, więc ten trójkąt jest równoramienny b) w ΔABC β=180−3α wΔMBC γ=180−α−β=180−α−(180−3α)=2α więc trójkąty MBC i ABC podobne na mocy cechy kąt−kąt. Jest ok?

wredulus_pospolitus: jest ok ... niepotrzebnie wyznaczasz β trójkąt ABC ma kąty: α, β, 2α trójkąt CBM ma kąty: α, β, γ stąd y = 2α

salamandra: no w sumie ta dzieki