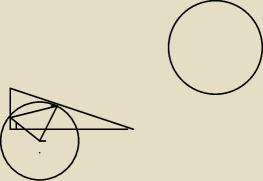Zadanie z trójkątem i okręgiem. Proszę o wskazówkę jak rozwiązać
Łukasz: W trójkącie prostokątnym przyprostokątne mają 12 cm i 16 cm. Oblicz długość okręgu
przechodzącego przez środek krótszej przyprostokątnej i stycznego do przeciwprostokątnej w jej
środku.
25 lut 16:32
miki: odcinek łączący środki boków trojkąta jet równoległy do trzeciego boku i =połowie tego boku
25 lut 17:47
miki:
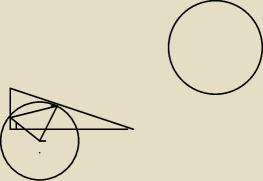
25 lut 17:53
miki: rysunek niedokładny nie umię pisać a tym bardziej rysować
25 lut 17:54
miki: r=40:6
4:r=40:6
25 lut 17:55
miki: 4:r=40:6
25 lut 17:56
miki: sory tylko pierwsza odpowiedż dobra r=40:6
25 lut 17:57
miki: jesteś?
25 lut 17:58
Łukasz: Dzięki miki za zainteresowanie. Na rysunku do zadania środek okręgu jest wewnątrz trójkąta, o
tym boku wiedziałem wcześniej, powstaje tam trójkąt równoramienny o ramionach r, ale dlaczego
r=40:6
25 lut 18:36
miki: nie potrafię opisywać rysunku
25 lut 18:45
miki: wylicz w małym trójkącie sin kąta
25 lut 18:46
miki: o bokach 6 i 10
25 lut 18:46
Łukasz: dzięki, ale musi być jakieś inne rozwiązanie bez stosowania funkcji sin, to zadanie dla
gimnazjalistów
25 lut 19:10
miki: trójkąty podobne
25 lut 20:38