trójkąt maturka20: Niech ABC bedzie trójkatem ostrokątnym z wysokoscią CD=h oraz niech O bedzie srodkiem okregu opisanego na tym trójkacie. Oblicz kąt ∡ CDO wiedząc że ∡ ABC=α oraz ∡ BCA=β.

f123: zrob rysunek, przypomnij sobie gdzie lezy srodek okregu opisanego na trojkacie. Jak juz te obie rzeczy zrobisz, zadanie staje sie banalne

maturka20: To jest punkt przecięcia symetralnych ale nadal nie wiem co dalej

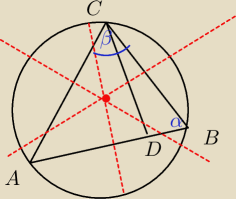
salamandra: coś takiego, taki rysunek?

maturka20: No tak rysunek ok i i nie wiem jak policzyc ten kąt CDO

salamandra: nie wiem, próbowałem coś z tw. sinusów, ale też nic nie wychodzi

f123: A po co z tw cosinusow, symetralne bokow sa pod katem prostym, moze to bedzie jakas podpowiedz

salamandra: {h}{sinα}=2R

	h
R=
	2sinα

wiemy, że CO i DO=R, ale co dalej

f123: Jak wroce do domu ci to napisze

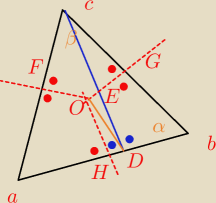
f123: kat BED = 180 − α kat FOG = 180 − β kat FOH = α − β kat OED = α kat HOD = α − 2β kat HDO = 90 − 2β − α a wiec kat CDO = 2β + α

f123: chyba tak to bedzie szlo

salamandra: Skąd masz ze FOG = 180−β?

salamandra: Jako czworokąt traktujesz tak?

maturka20: Możesz wyjaśnić jak policzyłeś BED

salamandra: Potraktował jak czworokąt− BDEG

f123: @salamandra czworokat CFOG

maturka20: A jak policzyłeś ten pierwszy kat BED

salamandra: Napisałem Ci

maturka20: Nadal nie wiem skąd ten BED

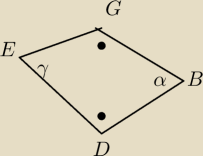
salamandra: 90+90+α+γ=360 180+α+γ=360 γ=180−α

maturka20: Ale to nie jest kat BED tak jak napisał f123

maturka20:

f123: To jest BED

f123: sory, GED

maturka20: ok a nie rozumiem czemu kat HOD = α − 2β Mogę prosić o wyjaśnienie?

maturka20: Nie wiem nadalczemu HOD=α − 2β Staram sie zrozumieć

f123: HOD = 360 − FOG − HOF − DEG

maturka20: Coraz bardzie sie gubie a czemu kat FOH = α − β ?

f123: kat FAD = 180 − α − β Czworokat FOHA: dwa katy proste (360 − 2 * 90 = 180) czyli 180 − α − β + FOH = 180 => FOH = α + β

maturka20: A napisałes wcześniej że FOH = α − β

maturka20: HOD = 360 − FOG − HOF − DEG, czemu tu odejmujesz kąt DEG?

f123: @maturka20 o shi... to cale zadanie poszlo, jak nie bedziesz miala za zle, rozpisze ci to dzisiaj rano, ale tu jedynie najprawdopodobniej sie zniemi wynik ostatecznego kata na 2β − α

f123: @maturak20 aby otrzymac kat HOD, musze odjac DEG tez

maturka20: Uff tak się nameczyłam żeby zrozumieć twoje rozwiązanie to 14:38 ale spoko poczekam do rana

f123: ciezko mi sie skupic przez kwarantanne i te atmosfere

maturka20: f123: @maturak20 aby otrzymac kat HOD, musze odjac DEG tez Nie rozumiem czemu musisz go odjąc

f123: sorry... DOG

maturka20: Wg mnie to HOD = 360 − FOG − HOF − DOE , tylko nie znam miary DOE

f123: znamy, zobacz czworokat a katem α i dwoma katami prostymi

maturka20: A ile wynosi DOG

f123: @maturka20 ja... zostaw to rozwiazanie i zapomnij o nim, teraz zobaczylem ze zle jest, no coz z rana postaram ci sie nowe napisac jak znajde...

maturka20: Ok bo już tracę nadzueję

wredulus_pospolitus: Rozumiem, że zadanie NIE JEST rozwiązane

maturka20: Niestety było o 14:38 ale nie rozumiałam jak policzył kąt HOD i nadal nie wiem.....

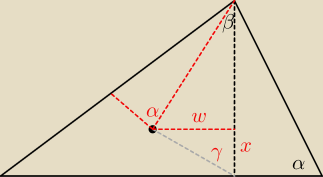
wredulus_pospolitus: Powiem tak ... mam rozwiązanie ... ale to są chooooolernie koszmarne przekształcenia, których nawet nie mam zamiaru o tej porze wypisywać. Ogólnie −−− wyznaczamy kolejne długości w tym trójkącie w zależności od 'h' oraz funkcji trygonometrycznych z α, β i wszelkimi kombinacjami z nimi związanymi (+/− +/− od kątów)

	w
w pewnym momencie będziemy w stanie wyznaczyć długości w i x ... kąt γ będzie arctg(		)
	x

No ale to z pewnością nie oto chodziło w tym zadaniu