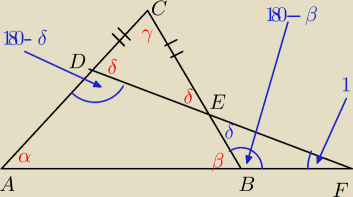
planimetria salamandra: Dany jest trójkąt ABC w którym AC>BC. Na bokach AC i BC tego trójkąta obrano odpowiednio punkty D i E takie, że zachodzi równość CD=CE. Proste AB i DE przecinają się w punkcie F. Wykaż, że ∡BAC=∡ABC−2*∡AFD nawypisywałem sobie już wszystkie kombinacje z tymi kątami ale nic nie wychodzi

wredulus_pospolitus: Katy ΔBEF 180 − β + 1 + δ = 180 −−−> δ = β − 1 Kąty ΔDEC γ = 180 − 2δ = 180 − 2β + 2* 1 Kąty ΔABC α = 180 − (β + γ) = 180 − β − 180 + 2β − 2* 1 = β − 2* 1

wredulus_pospolitus: Salamandra ... a teraz Ciebie dobiję −−− ja nie widziałem rozwiązania ... po prostu sobie wyznaczałem inne kąty za pomocą β i 1

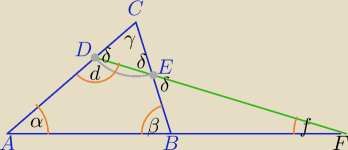
Mila: α=β−2f ? ======= 1) β=f+δ− kąt zewnętrzy Δ (ΔBFE) jest równy sumie kątów Δ do niego nieprzyległych δ=β−f 2) α+d+f=180 i d+δ=180 stąd: α+f=δ α+f=β−f α=β−2f ======

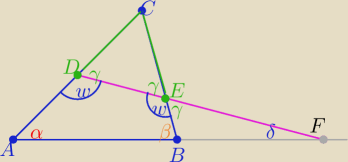
Eta: (*) β= γ+δ −− miara kąta zewnętrznego w=180^o−γ −− miara kąta przyległego to α+w+w+β=360^o ⇒ α=2γ− δ i z (*) γ=β−δ to α= β−2δ ====== c.n.w.

Eta: 2 min. spóźnienia

Mila:

salamandra: dziękuję Wam, ja napiszę do czego ja tylko doszedłem γ=180−2δ α=180−(180−2δ−β)=2δ+β 1=180−(180−β−δ)=β+δ i nie wiedziałem jak to wykorzystać

wredulus_pospolitus: z ostatniego wyznacz δ i podstaw do środkowego

wredulus_pospolitus: ale masz źle w ostatnim podstawieniu 1 = 180 − (180 − β) −δ = β − δ

salamandra: tak, fakt, ten nawias powinien tylko obejmować (180−β), już poprawiam i zobaczę co wskóram

salamandra: 1=β−δ δ=β−1 α chyba też mam źle, tak teraz patrzę skąd ja to w ogóle wziąłem

salamandra: a nie, ok, z ABC wziąłem

salamandra: α=180−(180−2δ)−β = 2δ−β α=2(β−1)−β = 2β−2*1−β = β−2*1 jednak w α też miałem błąd, β poza nawiasem powinno być