planimetria - z gwiazdką
salamandra: Oblicz sinus jednego z kątów ostrych trójkąta prostokątnego wiedząc, że stosunek długości
promienia okręgu wpisanego w ten trójkąt do promienia okręgu opisanego na tym trójkącie jest
równy 0,4
4r=R
muszę jakoś przyprostokątną/przeciwprostokątną uzależnić od
przeciwprostokątnej/przyprostokątnej

27 mar 17:57
salamandra: | | 1 | | 2 | |
oczywiście nie |
| , tylko |
| , więc 5r=2R |
| | 4 | | 5 | |
27 mar 18:04
Saizou : i Pitagoras

27 mar 18:08
salamandra: 5r=c
co mogę z tego wskórać? Chyba jeszcze nie Pitagoras

27 mar 18:12
Mila:
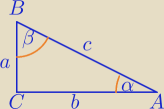
c=2R
a+b=2r+2R
========
a+b=7r
a
2+b
2=(5r)
2
==========
b=7r−a >0⇔7r>a
a
2+(7r−a)
2=25r
2
oblicz a, potem b i to wszystko będzie
27 mar 18:17
salamandra: a+b=2r+2R

z tych odcinków stycznych itp to jest rozumiem?
27 mar 18:20
Saizou :
5r=2R
5a+5b−5c=2c
5a+5b=7c
a
2+b
2=c
2
49a
2+49b
2=25a
2+50ab+25b
2
| | a | |
uporządkuj i podziel przez b2 oraz podstaw |
| =t |
| | b | |
27 mar 18:20
salamandra: mógłbym równie dobrze podzielic przez a2?
27 mar 18:24
Saizou : Tak, to bez znaczenia, bo równanie jest symetryczne
27 mar 18:25
ZKS:
Mógłbyś nawet nie dzielić.

27 mar 18:26
salamandra: w życiu bym nie pomyślał, żeby dzielić przez b2 jak mam dwie niewiadome i jeszcze 50ab
27 mar 18:26
ZKS:
24a2 − 50ab + 24b2 = 0
Δa = (25b)2 − (24b)2 = (25 + 24)(25 − 24) = 49b
√Δa = 7b
27 mar 18:29
salamandra: | | 3 | | 4 | |
wyszło mi t= |
| v t= |
| . i to są tangensy tych kątów, teraz po prostu na sinus to? |
| | 4 | | 3 | |
27 mar 18:29
Mila:
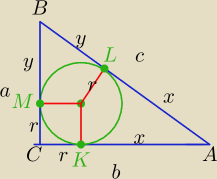
Tw. ( było na forum)
Suma dł. przyprostokątnych jest równa sumie średnic okręgu wpisanego i opisanego na tym Δ .
a+b=2r+x+y⇔
a+b=2r+c
a+b=2r+2R
27 mar 18:29
salamandra: Domyśliłem się Milu, ale dziękuję

27 mar 18:30
Saizou :
jak jeszcze ustalisz sobie kolejność np. a<b
to wystarczy rozważyć jeden przypadek

27 mar 18:31
salamandra: głupie pytanie pewnie zadam, ale żeby tg zamienić na sin/cos, to zawsze obliczałem "r" i wtedy
| | y | |
wstawiałem do sinα= |
| , trochę "podstawówkowo" robię, czy nie ma innej możliwości? |
| | r | |
27 mar 18:32
Saizou :
Teraz masz zadanie typu:
| | 3 | |
Niech tg α= |
| , gdzie α jest kątem ostrym. Oblicz sinus kąta α. |
| | 4 | |
Narysuj trójkąt o przyprostokątnych
3x oraz 4x
i `Pitagoras
27 mar 18:34
salamandra: no teoretycznie to samo

27 mar 18:37
ZKS:
| | tg(x) | |
sin(x) = ± |
| |
| | √tg2(x) + 1 | |
27 mar 18:38
salamandra: @ZKS władasz dziś takimi wzorami, że tylko bardziej się utwierdzam w przekonaniu, jak mało
jeszcze umiem


27 mar 18:39
ZKS:
Zobacz, to nie jest trudne:
| | sin2(x) | | sin2(x) + cos2(x) | | 1 | |
tg2(x) + 1 = |
| + 1 = |
| = |
| . |
| | cos2(x) | | cos2(x) | | cos2(x) | |

27 mar 18:41
Saizou :
salamandra nikt wszystkiego nie wie

27 mar 18:41
ZKS:
Otrzymujesz zatem:
| | 1 | | 1 | |
cos2(x) = |
| ⇒ cos(x) = ± |
| . |
| | tg2(x) + 1 | | √tg2(x) + 1 | |
Tak samo zrób z sin(x).
27 mar 18:42
ZKS:
Saizou doktoryzujesz się?

27 mar 18:43
Saizou :
NIe, jakoś z bardzo teoretycznie się dla mnie zrobiło

zwłaszcza po algebrze i topologii

27 mar 18:45
ZKS:
Pewnie w takim razie w banku jakimś pracujesz?

27 mar 18:52
Saizou :
to Cię zdziwię, bo obecnie nie pracuję

27 mar 18:53
ZKS:
Nic ciekawego nie ma na rynku pracy? Rozumiem, że magisterkę już masz?
27 mar 18:55
Saizou : Tak, ale jakoś nie czuję się, że to było coś mego ważnego
27 mar 19:03
ZKS:
Praca, czy magisterka.

27 mar 19:08
Saizou : To i to

27 mar 19:08
ZKS:
Na końcu oczywiście miałbyć znak zapytania.

27 mar 19:08
Saizou :
Myślę, czy nie wrócić do szkoły, ale jako informatyk w SP albo matma w LO.
Na razie to korki, chociaż obecnie jest ciężko.
Magisterka obroniona na 5

27 mar 19:10
ZKS:
Nie czujesz potrzeby, aby pracować?
27 mar 19:10
ZKS:
Gratulacje w takim razie.


27 mar 19:11
ZKS:
Sam myśle, czy czasem nie dawać korepetycji, ale jakoś czuję się za głupi na to.

27 mar 19:12
Saizou :
cały czas o tym myślę, ale obecna sytuacja nie sprzyja.
Z korków można całkiem sporo wyciągnąć.
Dzięki.
27 mar 19:13
ZKS:
Niestety nie sprzyja. Ciekawe ile czasu jeszcze to potrwa.
27 mar 19:14
Saizou :
ZKS warto spróbować, weź sobie najpierw jednego podopiecznego.
27 mar 19:14
Saizou :
Ostatnio oglądałem lajw z wirusologiem na yt i szacuje się, że w "ciepłych"
miesiącach powinno się unormować.
Szczepionka jak już to w przyszłym roku, w drugiej połowie.
27 mar 19:16
ZKS:
W tym czasie pewnie nikt nie będzie za bardzo, chętny.

Ile bierzesz za 1h?
27 mar 19:17
Saizou :
To już niech pozostaje tajemnica tutaj na forum

Ale po tym jak się wszystko unormuje.
27 mar 19:18
f123: Mozna korepetycje / zajecia prowadzic przez internet, jednak jest to malo skuteczne. Sporo osob
ma problem z koncentracja
27 mar 19:19
f123: @Saizou szyczyt epidemi przewidywany jest na poczatek maja
27 mar 19:19
f123: sory panowie ze sie tak wcinam
27 mar 19:19
ZKS:
Może inaczej zapytam. Ile na początku kariery korepetytorskiej, bo nawet nie wiem ile w razie
czego,krzyczeć.

27 mar 19:21
f123: @ZKS moja mama bierze 100zl za 1 godzine
27 mar 19:21
salamandra: naprawdę są takie wysokie stawki?
27 mar 19:22
f123: zalezy jak kto sobie ustawi, 100zl za godzine matematyki to w sumie norma
27 mar 19:23
Saizou :
Na dzień dobry, możesz zaproponować 1 zł/ min

to wg mnie takie minimum.
27 mar 19:23
ZKS:
O kurdę to niezłe stawki się teraz zrobiły.

27 mar 19:27
salamandra: godzina mija w mgnieniu oka
27 mar 19:27
ZKS:
salamandra żebyś się nie nudził trzymaj:
| | x + a | | y | |
Nie wychodząc od tezy udowodnij nierówność |
| + |
| > 2 dla y > x > 0 ∧ a > 0. |
| | y + a | | x | |
Matura 2019.

27 mar 19:28
ZKS:
Tylko Ty
Saizou masz tytuł magistra z matmatyki to możesz tyle krzyknąć. Niestety ja
mam tytuł z czego innego.

27 mar 19:30
Saizou : dlatego piszę, że 60 zł/60 min to taka dobra cena na początek.
27 mar 19:31
ZKS:
Rozumiem, w takim razie trzeba będzie sobie w razie czego, co nie co po przypominać.

27 mar 19:35
f123: @ZKS matura 2019 z matematyki rozszerzonej byla prosta, a to zadanie ze dali na maturze to
jakis zart

(dla nas dla maturzystow to dobrze, bo darmowe punkty)
27 mar 19:39
ZKS:
W jaki sposób zrobiłeś to zadanie?

27 mar 19:43
Saizou :
f123 to złap taki zadanie.
Wykaż, że jeżeli m, n ≥ 2 są liczbami całkowitymi, to
| 1 | | 1 | |
| + |
| > 1 |
| (m+1)1/n | | (n+1)1/m | |
27 mar 19:43
f123: @Saizou narazie nie mam pomyslu, przy okazji wchodzi w gre podstawienie skrajnego przypadku?
Czyli m = n = 2 i pokazac ze ejst to wieksze od 1?
27 mar 19:54
Saizou :
podpowiem, że można to łatwo zrobić z nierówności między średnimi.
27 mar 19:55
salamandra: co to jest ta cała nierównośc między średnimi? wiele razy to rekomendujecie, ale to też chyba
wykracza poza podstawę technikum?
27 mar 19:56
f123: Tak, ale przy zaleznosci miedzy srednimi mamy wszedzie znak >= a tutaj jest tylko >
27 mar 19:56
f123: @salamandra najczesciej korzysta sie z zaleznosci miedzy srednia geometryczna a srednia
arytmetyczna, mam na to pare maturalnych zadan dowodowych, moge tutaj podrzucic
27 mar 19:57
Saizou :
ale skoro zachodzi nierówność słaba (≥), to tym bardziej zachodzi nierówność ostra (>)
27 mar 19:57
salamandra: średnia geometryczna też mi "obco" brzmi

27 mar 19:59
f123: @salamandra w karcie wzorow jest, strona 10
27 mar 19:59
salamandra: na 18−tej

mimo to, nie przypomina mi się, abym z tego korzystał (statystyka w 1 klasie)
27 mar 20:01
Saizou :
W ciągu geometrycznym jest

Niech (a,b,c) − ciąg geometryczny
b=
√ac
√ac średnia geometryczna

27 mar 20:02
salamandra: to to już znam

27 mar 20:03
f123: @saizou wyszlo mi, skorzystalem z zaleznosci miedzy srednia arytmetyczna a geomtryczna, napisze
tu rozwiazanie jak rozkminie tutaj wszystkie funkcje, bo jeszcze nie umiem tak tego
przejrzyscie napisac jak ty. Jak zrobiles taki wykladnik?
27 mar 20:03
Saizou :
jest to ułamek w potędze, ale ułamek zapisany jako 1 / n
27 mar 20:06
f123: @Saizou widze, dobra ide sie przejsc, wracam, i pisze rozwiazanie
27 mar 20:07



 c=2R
c=2R
 z tych odcinków stycznych itp to jest rozumiem?
z tych odcinków stycznych itp to jest rozumiem?

 Tw. ( było na forum)
Suma dł. przyprostokątnych jest równa sumie średnic okręgu wpisanego i opisanego na tym Δ .
a+b=2r+x+y⇔
a+b=2r+c
a+b=2r+2R
Tw. ( było na forum)
Suma dł. przyprostokątnych jest równa sumie średnic okręgu wpisanego i opisanego na tym Δ .
a+b=2r+x+y⇔
a+b=2r+c
a+b=2r+2R








 zwłaszcza po algebrze i topologii
zwłaszcza po algebrze i topologii 









 Ile bierzesz za 1h?
Ile bierzesz za 1h?
 Ale po tym jak się wszystko unormuje.
Ale po tym jak się wszystko unormuje.

 to wg mnie takie minimum.
to wg mnie takie minimum.




 (dla nas dla maturzystow to dobrze, bo darmowe punkty)
(dla nas dla maturzystow to dobrze, bo darmowe punkty)


 mimo to, nie przypomina mi się, abym z tego korzystał (statystyka w 1 klasie)
mimo to, nie przypomina mi się, abym z tego korzystał (statystyka w 1 klasie)
 Niech (a,b,c) − ciąg geometryczny
b=√ac
√ac średnia geometryczna
Niech (a,b,c) − ciąg geometryczny
b=√ac
√ac średnia geometryczna 
